题目内容
3. 已知:如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,且AD=DC.
已知:如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,且AD=DC.(1)求证:AB=BC;
(2)过点B作⊙O的切线,交AC的延长线于点F,且CF=DC,求sin∠CAE的值.
分析 (1)由AB为直径,根据圆周角的性质,可得BD⊥AC,又由AD=DC,根据线段垂直平分线的性质,即可证得AB=BC;
(2)由BF切⊙O于点B,易证得△ABD∽△BFD,然后由相似三角形的对应边成比例,求得BD的长,继而求得答案.
解答 (1)证明:∵AB为⊙O的直径,
∴∠ADB=90°,
又∵AD=DC,
∴AB=BC;
(2)解:∵BF切⊙O于点B,
∴∠ABF=90°,
∴∠BAF+∠F=90°.
又∵∠BAF+∠ABD=90°,
∴∠ABD=∠F,
∴△ABD∽△BFD,
∴$\frac{AD}{BD}=\frac{BD}{DF}$,
∴BD2=AD•DF.
又∵CF=DC,
∴CF=DC=AD,
设CF=DC=AD=k,
则BD2=AD•DF=k•2k=2k2,
∴$BD=\sqrt{2}k$.
在Rt△BCD中,$BC=\sqrt{3}k$,$sin∠CBD=\frac{k}{{\sqrt{3}k}}=\frac{{\sqrt{3}}}{3}$,
又∵∠CBD=∠CAE,
∴$sin∠CAE=\frac{{\sqrt{3}}}{3}$.
点评 此题考查了切线的性质,圆周角定理、相似三角形的判定与性质以及三角函数等知识.注意证得△ABD∽△BFD是关键.

练习册系列答案
相关题目
11. 如图,△ABC内接于⊙O,AB=8,BC=10,AC=6,D是弧AB的中点,连接CD交AB于点E,则DE:CE等于( )
如图,△ABC内接于⊙O,AB=8,BC=10,AC=6,D是弧AB的中点,连接CD交AB于点E,则DE:CE等于( )
 如图,△ABC内接于⊙O,AB=8,BC=10,AC=6,D是弧AB的中点,连接CD交AB于点E,则DE:CE等于( )
如图,△ABC内接于⊙O,AB=8,BC=10,AC=6,D是弧AB的中点,连接CD交AB于点E,则DE:CE等于( )| A. | 2:5 | B. | 1:3 | C. | 2:7 | D. | 1:4 |
4.两条直线被第三条直线所截.下列叙述正确的是( )
| A. | 同位角一定不相等 | B. | 内错角的对顶角-定相等 | ||
| C. | 同位角的邻补角一定相等 | D. | 两对同旁内角的和一定大于180° |
5.下列解方程正确的是( )
| A. | 由4x-6=2x+3移项得4x+2x=3-6 | |
| B. | 由$\frac{4}{7}x=5-\frac{x-1}{7}$,去分母得4x=5-x-1 | |
| C. | 由2(x+3)-3(x-1)=7,去括号得 2x+3-3x+1=7 | |
| D. | 由$\frac{x}{0.3}-0.5=x$得 $\frac{10x}{3}-\frac{1}{2}=x$ |
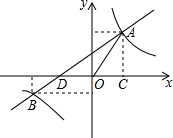 如图,在平面直角坐标系中,双曲线y=$\frac{m}{x}$与直线y=kx+b相交于A、B两点,过点A作AC⊥x轴于点C,其中AC=4,tan∠AOC=$\frac{4}{3}$且点B的坐标为(-6,n).
如图,在平面直角坐标系中,双曲线y=$\frac{m}{x}$与直线y=kx+b相交于A、B两点,过点A作AC⊥x轴于点C,其中AC=4,tan∠AOC=$\frac{4}{3}$且点B的坐标为(-6,n).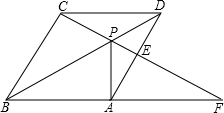 如图,点P是菱形ABCD对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于F,
如图,点P是菱形ABCD对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于F,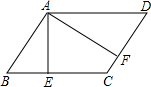 如图,已知平行四边形ABCD的周长是80cm,BC=24cm,AE=12cm
如图,已知平行四边形ABCD的周长是80cm,BC=24cm,AE=12cm