题目内容
1．
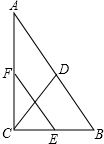如图，在Rt△ABC中，∠ACB=90°，点D、E、F分別为AB，AC，BC的中点，若CD=5，則EF的长为5．
分析 已知CD是Rt△ABC斜边AB的中线，那么AB=2CD；EF是△ABC的中位线，则EF应等于AB的一半．
解答 解：∵△ABC是直角三角形，CD是斜边的中线，
∴CD=$\frac{1}{2}$AB，
又∵EF是△ABC的中位线，
∴AB=2CD=2×5=10，
∴EF=$\frac{1}{2}$×10=5．
故答案为：5
点评 此题主要考查了三角形中位线定理以及直角三角形斜边上的中线等知识，用到的知识点为：（1）直角三角形斜边的中线等于斜边的一半；（2）三角形的中位线等于对应边的一半．
练习册系列答案
阅读快车系列答案
相关题目
11．
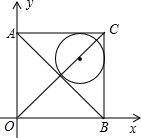如图，在平面直角坐标系中有一正方形AOBC，反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点，半径为4-2$\sqrt{2}$的圆内切于△ABC，则k的值为（ ）
如图，在平面直角坐标系中有一正方形AOBC，反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点，半径为4-2$\sqrt{2}$的圆内切于△ABC，则k的值为（ ）| A． | $\sqrt{2}$ | B． | 2 | C． | 4 | D． | 2$\sqrt{2}$ |
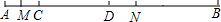如图，已知线段AB=14，在AB上有C，D，M，N四点，且满足AC：CD：DB=1：2：4，AC=2AM，DB=4DN．求：MN的长度．
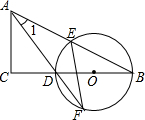如图，在△ABC中，∠C=90°，D是BC边上一点，以DB为直径的⊙O经过AB的中点E，交AD的延长线于点F，连结EF．
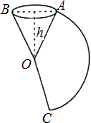如图，把一个圆锥沿母线OA剪开，展开后得到扇形AOC，已知圆锥的高h为12cm，OA=13cm，则扇形AOC中$\widehat{AC}$的长是10πcm（计算结果保留π）．