题目内容
13.有3张不透明的卡片,除正面写有不同的数字外,其它均相同,将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式y=kx+b(k≠0,k、b为常数)中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b.(1)写出k为负数的概率;
(2)求一次函数y=kx+b的图象经过二、三、四象限的概率.(用树状图或列表法求解)
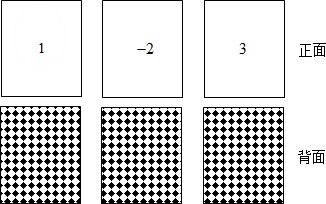
分析 (1)三张牌中负数只有一个,为-2,求出k为负数的概率即可;
(2)根据题意列表得出所有等可能的情况数,找出符合题意的情况数,即可求出所求概率.
解答 解:(1)k为负数的概率是$\frac{1}{3}$;
(2)根据题意列表如下:
| 1 | -2 | 3 | |
| 1 | ---- | (1,-2) | (1,3) |
| -2 | (-2,1) | ---- | (-2,3) |
| 3 | (3,-1) | (3,-2) | ---- |
∴一次函数y=kx+b经过第一、三、四象限的概率为$\frac{2}{6}$=$\frac{1}{3}$.
点评 此题考查了列表法与树状图法,概率=所求情况数与总情况数之比.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
4.下列事件是必然事件的为( )
| A. | 相等的圆周角所对的弧相等 | |
| B. | 方程x2-x+1=0有两个不等实根 | |
| C. | 同一个角的正弦值和余弦值的和等于1 | |
| D. | 圆的切线垂直于过切点的半径 |
8.国家发改委决定,自2015年6月1日起全面放开药品价格,在市场机制作用下,今年春节后3月1日起,部分常用抗生素药品零售价出现下降,合肥某药房对售出的涉及降价的抗生素药品中A、B、C、D药的售价变化及今年2月份抗生素销量情况进行了统计,并绘制成如下统计图:
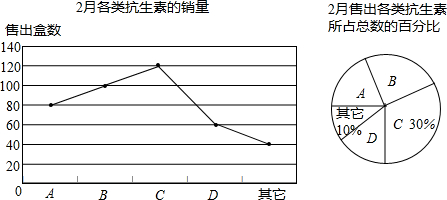
(1)2月份该药房共售出抗生素400盒;若3月份各种抗生素的销量按2月份的销量计算,则3月份A、B、C、D四种抗生素的销售额比2月份减少了904元;
(2)补全扇形统计图;
(3)吴老师到该药房买一些抗生素作为家里备用药,在A、B、C、D各一盒中随机购买两盒,请用画树状图或列表法求出他刚好选中A和B的概率.

| A | B | C | D | |
| 2月份售价(元/盒) | 15.4 | 8.6 | 11.2 | 28.2 |
| 3月份售价(元/盒) | 12.8 | 7.7 | 10 | 20.5 |
(2)补全扇形统计图;
(3)吴老师到该药房买一些抗生素作为家里备用药,在A、B、C、D各一盒中随机购买两盒,请用画树状图或列表法求出他刚好选中A和B的概率.
18.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
请估计:
(1)当n很大时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)假如你去摸一次,你摸到白球的概率是0.6,摸到黑球的概率是0.4;
(3)试估算口袋中黑球有多少只?
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
| 摸到白球的频率$\frac{m}{n}$ | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)当n很大时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)假如你去摸一次,你摸到白球的概率是0.6,摸到黑球的概率是0.4;
(3)试估算口袋中黑球有多少只?
2.某企业今年3月份产值为a万元,4月份比3月份减少了10%,5月份比4月份增加了15%,则5月份的产值是( )
| A. | (a-10%)(a+15%)万元 | B. | a(1-90%)(1+85%)万元 | C. | a(1-10%)(1+15%)万元 | D. | a(1-10%+15%)万元 |
3.某种油菜籽在相同条件下的发芽试验结果如下:
由此可以估计油菜籽发芽的概率约为0.95(精确到0.01),其依据是频率的稳定性.
| 每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2020 | 3000 |
| 发芽的频数m | 96 | 283 | 344 | 552 | 948 | 1912 | 2848 |
| 发芽的频率 | 0.96 | 0.94 | 0.86 | 0.92 | 0.95 | 0.95 | 0.95 |
 如图,四边形OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的一支上,分别过点A,C作x轴的垂线,垂足分别为M和N,则有以下结论:
如图,四边形OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的一支上,分别过点A,C作x轴的垂线,垂足分别为M和N,则有以下结论: 如图,在Rt△ABC中,∠ACB=90°,点D、E、F分別为AB,AC,BC的中点,若CD=5,則EF的长为5.
如图,在Rt△ABC中,∠ACB=90°,点D、E、F分別为AB,AC,BC的中点,若CD=5,則EF的长为5. 如图,正六边形ABCDEF内接于半径为3的圆O,则劣弧AB的长度为π.
如图,正六边形ABCDEF内接于半径为3的圆O,则劣弧AB的长度为π.