题目内容
10.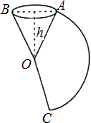 如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中$\widehat{AC}$的长是10πcm(计算结果保留π).
如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中$\widehat{AC}$的长是10πcm(计算结果保留π).
分析 根据$\widehat{AC}$的长就是圆锥的底面周长即可求解.
解答 解:∵圆锥的高h为12cm,OA=13cm,
∴圆锥的底面半径为$\sqrt{1{3}^{2}-1{2}^{2}}$=5cm,
∴圆锥的底面周长为10πcm,
∴扇形AOC中$\widehat{AC}$的长是10πcm,
故答案为:10π.
点评 本题考查了圆锥的计算,解题的关键是了解圆锥的底面周长等于展开扇形的弧长,难度不大.

练习册系列答案
相关题目
18.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
请估计:
(1)当n很大时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)假如你去摸一次,你摸到白球的概率是0.6,摸到黑球的概率是0.4;
(3)试估算口袋中黑球有多少只?
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
| 摸到白球的频率$\frac{m}{n}$ | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)当n很大时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)假如你去摸一次,你摸到白球的概率是0.6,摸到黑球的概率是0.4;
(3)试估算口袋中黑球有多少只?
2.某企业今年3月份产值为a万元,4月份比3月份减少了10%,5月份比4月份增加了15%,则5月份的产值是( )
| A. | (a-10%)(a+15%)万元 | B. | a(1-90%)(1+85%)万元 | C. | a(1-10%)(1+15%)万元 | D. | a(1-10%+15%)万元 |
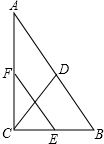 如图,在Rt△ABC中,∠ACB=90°,点D、E、F分別为AB,AC,BC的中点,若CD=5,則EF的长为5.
如图,在Rt△ABC中,∠ACB=90°,点D、E、F分別为AB,AC,BC的中点,若CD=5,則EF的长为5. 如图,正六边形ABCDEF内接于半径为3的圆O,则劣弧AB的长度为π.
如图,正六边形ABCDEF内接于半径为3的圆O,则劣弧AB的长度为π.