题目内容
11.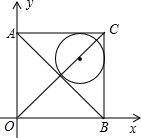 如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为4-2$\sqrt{2}$的圆内切于△ABC,则k的值为( )
如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为4-2$\sqrt{2}$的圆内切于△ABC,则k的值为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 4 | D. | 2$\sqrt{2}$ |
分析 根据正方形的性质得出AD=BD=DO=CD,NO=DN,HQ=QE,HC=CE,进而根据半径为(4-2$\sqrt{2}$)的圆内切于△ABC,得出CD的长,从而得出DO的长,再利用勾股定理得出DN的长进而得出k的值.
解答 解:设正方形对角线交点为D,过点D作DM⊥AO于点M,DN⊥BO于点N;
设圆心为Q,切点为H、E,连接QH、QE.
∵在正方形AOBC中,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,
∴AD=BD=DO=CD,NO=DN,HQ=QE,HC=CE,
QH⊥AC,QE⊥BC,∠ACB=90°,
∴四边形HQEC是正方形,
∵半径为(4-2$\sqrt{2}$)的圆内切于△ABC,
∴DO=CD,
∵HQ2+HC2=QC2,
∴2HQ2=QC2=2×(4-2$\sqrt{2}$)2,
∴QC2=48-32$\sqrt{2}$=(4$\sqrt{2}$-4)2,
∴QC=4$\sqrt{2}$-4,
∴CD=4$\sqrt{2}$-4+(4-2$\sqrt{2}$)=2$\sqrt{2}$,
∴DO=2$\sqrt{2}$,
∵NO2+DN2=DO2=(2$\sqrt{2}$)2=8,
∴2NO2=8,
∴NO2=4,
∴DN×NO=4,
即:xy=k=4.
故选C.
点评 此题主要考查了正方形的性质以及三角形内切圆的性质以及待定系数法求反比例函数解析式,根据已知求出CD的长度,进而得出DN×NO=4是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.函数y=$\frac{1}{x-2}$的自变量x的取值范围为( )
| A. | x>2 | B. | x<2 | C. | x≤2 | D. | x≠2 |
19.小红、小明在玩“剪子、包袱、锤子”游戏,小红给自己一个规定:一直不出“锤子”.小红、小明获胜的概率分别是P1,P2,则下列结论正确的是( )
| A. | P1=P2 | B. | P1>P2 | C. | P1<P2 | D. | P1≤P2 |
6. 如图,已知矩形ABCD中,R、P分别是DC、BC上的点,E、F分别是AP、RP的中点,当点P在BC上从B向C移动而R不动时,那么下列结论成立的是( )
如图,已知矩形ABCD中,R、P分别是DC、BC上的点,E、F分别是AP、RP的中点,当点P在BC上从B向C移动而R不动时,那么下列结论成立的是( )
 如图,已知矩形ABCD中,R、P分别是DC、BC上的点,E、F分别是AP、RP的中点,当点P在BC上从B向C移动而R不动时,那么下列结论成立的是( )
如图,已知矩形ABCD中,R、P分别是DC、BC上的点,E、F分别是AP、RP的中点,当点P在BC上从B向C移动而R不动时,那么下列结论成立的是( )| A. | 线段EF的长不能确定 | B. | 线段EF的长逐渐增大 | ||
| C. | 线段EF的长逐渐减小 | D. | 线段EF的长不改变 |
 如图,已知线段AB=6cm,延长线段AB到C,使BC=2AB,若点D是AC上一点,且AD比DC短4cm,点E是BC的中点,求线段DE的长.
如图,已知线段AB=6cm,延长线段AB到C,使BC=2AB,若点D是AC上一点,且AD比DC短4cm,点E是BC的中点,求线段DE的长. 如图,四边形OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的一支上,分别过点A,C作x轴的垂线,垂足分别为M和N,则有以下结论:
如图,四边形OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的一支上,分别过点A,C作x轴的垂线,垂足分别为M和N,则有以下结论: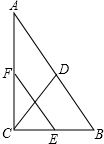 如图,在Rt△ABC中,∠ACB=90°,点D、E、F分別为AB,AC,BC的中点,若CD=5,則EF的长为5.
如图,在Rt△ABC中,∠ACB=90°,点D、E、F分別为AB,AC,BC的中点,若CD=5,則EF的长为5.