题目内容
6.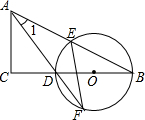 如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.
如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.(1)求证:∠1=∠F.
(2)若sinB=$\frac{\sqrt{5}}{5}$,EF=2$\sqrt{5}$,求CD的长.
分析 (1)连接DE,由BD是⊙O的直径,得到∠DEB=90°,由于E是AB的中点,得到DA=DB,根据等腰三角形的性质得到∠1=∠B等量代换即可得到结论;
(2)根据等腰三角形的判定定理得到AE=EF=2$\sqrt{5}$,推出AB=2AE=4$\sqrt{5}$,在Rt△ABC中,根据勾股定理得到BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=8,设CD=x,则AD=BD=8-x,根据勾股定理列方程即可得到结论.
解答 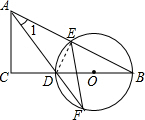 解:(1)证明:连接DE,
解:(1)证明:连接DE,
∵BD是⊙O的直径,
∴∠DEB=90°,
∵E是AB的中点,
∴DA=DB,
∴∠1=∠B,
∵∠B=∠F,
∴∠1=∠F;
(2)∵∠1=∠F,
∴AE=EF=2$\sqrt{5}$,
∴AB=2AE=4$\sqrt{5}$,
在Rt△ABC中,AC=AB•sinB=4,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=8,
设CD=x,则AD=BD=8-x,
∵AC2+CD2=AD2,
即42+x2=(8-x)2,
∴x=3,即CD=3.
点评 本题考查了圆周角定理,解直角三角形的性质,等腰三角形的性质,勾股定理,正确的作出辅助线构造直角三角形是解题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
16.在一个密闭不透明的袋子里有若干个白球.为估计白球个数,小何向其中投入8个黑球,搅拌均匀后随机摸出一个球,记下颜色,再把它放入袋中,不断重复摸球400次,其中88次摸到黑球,则估计袋中大约有白球( )
| A. | 18个 | B. | 28个 | C. | 36个 | D. | 42个 |
11. 如图,已知一块圆心角为270°的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是( )
如图,已知一块圆心角为270°的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是( )
 如图,已知一块圆心角为270°的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是( )
如图,已知一块圆心角为270°的扇形铁皮,用它作一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是( )| A. | 40cm | B. | 50cm | C. | 60cm | D. | 80cm |
18.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
请估计:
(1)当n很大时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)假如你去摸一次,你摸到白球的概率是0.6,摸到黑球的概率是0.4;
(3)试估算口袋中黑球有多少只?
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
| 摸到白球的频率$\frac{m}{n}$ | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)当n很大时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)假如你去摸一次,你摸到白球的概率是0.6,摸到黑球的概率是0.4;
(3)试估算口袋中黑球有多少只?
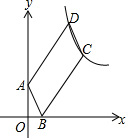 如图,在直角坐标系中,平行四边形ABCD的顶点A(0,2)、B(1,0)在x轴、y轴上,另两个顶点C、D在第一象限内,且AD=3AB.若反比例函数$y=\frac{k}{x}$(k>0)的图象经过C,D两点,则k的值是24.
如图,在直角坐标系中,平行四边形ABCD的顶点A(0,2)、B(1,0)在x轴、y轴上,另两个顶点C、D在第一象限内,且AD=3AB.若反比例函数$y=\frac{k}{x}$(k>0)的图象经过C,D两点,则k的值是24. 如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为“平行一次函数”.
如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为“平行一次函数”.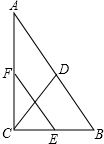 如图,在Rt△ABC中,∠ACB=90°,点D、E、F分別为AB,AC,BC的中点,若CD=5,則EF的长为5.
如图,在Rt△ABC中,∠ACB=90°,点D、E、F分別为AB,AC,BC的中点,若CD=5,則EF的长为5.