题目内容
1. 如图,从以下四个条件:①BC=EC; ②AC=DC;③∠DCA=∠ECB; ④AB=DE.
如图,从以下四个条件:①BC=EC; ②AC=DC;③∠DCA=∠ECB; ④AB=DE.(1)任取三个为条件,余下一个为结论,则最多可以构成正确的结论的个数是2个;
(2)选择其中一个正确的结论进行证明.
分析 在4个条件中任取三个条件,共有4种情况,然后根据全等三角形的判定条件即可求出答案.
解答 解:(1)任取三个为条件,余下一个为结论,正确的由①②③;①②④;
(2)在△ABC与△DEC中,
$\left\{\begin{array}{l}{AB=DE}\\{BC=EC}\\{AC=DC}\end{array}\right.$,
∴△ABC≌△DEC(SSS)
∴∠BCA=∠ECD,
∴∠BCA-∠ECA=∠ECD-∠ECA
∴∠BCE=∠ACD
故答案为:(1)2;
点评 本题考查全等三角形的判定,解题的关键是找出所有情况出来,然后根据全等三角形的条件进行判断.

练习册系列答案
相关题目
6. 如图,AC=AD,BC=BD,则下列判断正确的是( )
如图,AC=AD,BC=BD,则下列判断正确的是( )
 如图,AC=AD,BC=BD,则下列判断正确的是( )
如图,AC=AD,BC=BD,则下列判断正确的是( )| A. | AB垂直平分CD | B. | CD垂直平分AB | ||
| C. | AB与CD互相垂直平分 | D. | CD平分∠ACB |
11.若点A(x,y)与点B(6,-5)在同一条平行于y轴的直线上,且点A到x轴距离等于7,则A的坐标是( )
| A. | (6,-7)或(-6,-7) | B. | (-6,7)或(-6,-7) | C. | (6,7)或(-6,-7) | D. | (6,7)或(6,-7) |
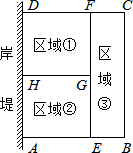 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为x米,矩形区域ABCD的面积为y米2.
为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为x米,矩形区域ABCD的面积为y米2.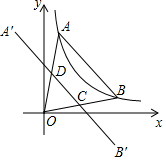 如图,点A、B在函数y=$\frac{1}{x}$(x>0)的图象上,点A在点B的左侧,且OA=OB,点A关于y轴的对称点为A′,点B关于x轴的对称点为B′,连接A′B′分别交OA、OB于点D、C.若四边形ABCD的面积为$\frac{6}{5}$,则点A的坐标为($\frac{1}{2}$,2),点C的坐标为($\frac{6}{5}$,$\frac{3}{10}$).
如图,点A、B在函数y=$\frac{1}{x}$(x>0)的图象上,点A在点B的左侧,且OA=OB,点A关于y轴的对称点为A′,点B关于x轴的对称点为B′,连接A′B′分别交OA、OB于点D、C.若四边形ABCD的面积为$\frac{6}{5}$,则点A的坐标为($\frac{1}{2}$,2),点C的坐标为($\frac{6}{5}$,$\frac{3}{10}$).