题目内容
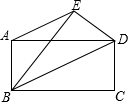 把矩形ABCD沿对角线BD折叠使点C落在点E处,连接AE,得到梯形ABDE,AB=12cm,BC=16cm,求梯形ABDE的面积.
把矩形ABCD沿对角线BD折叠使点C落在点E处,连接AE,得到梯形ABDE,AB=12cm,BC=16cm,求梯形ABDE的面积.考点:翻折变换(折叠问题)
专题:
分析:根据矩形的性质得AD=BC=16cm,AB=DC=12cm,AD∥BC,根据勾股定理可计算出BD=20cm,再根据折叠的性质得∠1=∠2,BE=BC=16cm,ED=DC=12cm,则∠1=∠3,所以BF=DF,又AD=BE,则AF=EF,所以∠4=∠5,于是∠1=∠5=∠4=∠3,得到BD∥AE,而AB=DE=12cm,且AB与DE不平行,所以可判断四边形ABDE是等腰梯形,过点A、E分别作AM⊥BD于点M、EN⊥BD于点N,则四边形AMNE为矩形,根据等腰图形的性质易得BM=DN,AE=MN,在Rt△ABD中,利用面积法克计算出AM=
=
,在Rt△ABM中,利用勾股定理计算出BM=
,则AE=MN=
,然后根据梯形的面积公式求解.
| 12×16 |
| 20 |
| 48 |
| 5 |
| 14 |
| 5 |
| 72 |
| 5 |
解答: 解:设BE与AD交于点F.
解:设BE与AD交于点F.
∵四边形ABCD为矩形,AB=12cm,BC=16cm,
∴AD=BC=16cm,AB=DC=12cm,AD∥BC,
∴BD=
=20cm,∠2=∠3,
∵把矩形ABCD沿对角线BD折叠,使点C落在点E处,
∴∠1=∠2,BE=BC=16cm,ED=DC=12cm,
∴∠1=∠3,
∴BF=DF,
∵BE=AD,
∴EF=AF,
∴∠4=∠5,
∴∠1=∠5=∠4=∠3,
∴AE∥BD,
∵AB=DE=12cm,且AB与DE不平行,
∴四边形ABDE是等腰梯形.
过点A、E分别作AM⊥BD于点M、EN⊥BD于点N,则四边形AMNE为矩形,
∴BM=DN,AE=MN,
在Rt△ABD中,
AM•BD=
AD•AB,则AM=
=
,
在Rt△ABM中,BM=
=
,
∴DN=
,
∴AE=MN=20-
-
=
,
∴梯形ABDE的面积=
(AE+BD)•AM=
(
+20)×
=
(cm2).
 解:设BE与AD交于点F.
解:设BE与AD交于点F.∵四边形ABCD为矩形,AB=12cm,BC=16cm,
∴AD=BC=16cm,AB=DC=12cm,AD∥BC,
∴BD=
| 162+122 |
∵把矩形ABCD沿对角线BD折叠,使点C落在点E处,
∴∠1=∠2,BE=BC=16cm,ED=DC=12cm,
∴∠1=∠3,
∴BF=DF,
∵BE=AD,
∴EF=AF,
∴∠4=∠5,
∴∠1=∠5=∠4=∠3,
∴AE∥BD,
∵AB=DE=12cm,且AB与DE不平行,
∴四边形ABDE是等腰梯形.
过点A、E分别作AM⊥BD于点M、EN⊥BD于点N,则四边形AMNE为矩形,
∴BM=DN,AE=MN,
在Rt△ABD中,
| 1 |
| 2 |
| 1 |
| 2 |
| 12×16 |
| 20 |
| 48 |
| 5 |
在Rt△ABM中,BM=
| AB2-AM2 |
| 14 |
| 5 |
∴DN=
| 14 |
| 5 |
∴AE=MN=20-
| 14 |
| 5 |
| 14 |
| 5 |
| 72 |
| 5 |
∴梯形ABDE的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 72 |
| 5 |
| 48 |
| 5 |
| 4128 |
| 25 |
点评:本题考查了折叠的性质:折叠前后两图形全等,即对应线段相等,对应角相等;也考查了勾股定理、矩形的性质以及等腰梯形的判定与性质.

练习册系列答案
相关题目
 如图,在△ABC中,AB=AC,AD⊥BC,CE⊥AB,AD=12,CE=8,求S△ABC.
如图,在△ABC中,AB=AC,AD⊥BC,CE⊥AB,AD=12,CE=8,求S△ABC.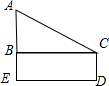 Rt△ABC中,∠ABC=90°,∠ACB=30°,四边形BCDE为矩形,且CD=
Rt△ABC中,∠ABC=90°,∠ACB=30°,四边形BCDE为矩形,且CD= 如图,已知PA、PB分别与⊙O相切于点A、B,点C在PB上,且CO∥PA,CD⊥PA于点D.
如图,已知PA、PB分别与⊙O相切于点A、B,点C在PB上,且CO∥PA,CD⊥PA于点D. 如图所示,Rt△ABC中,∠ACB=90°,∠BAC=45°,AD为∠BAC平分线交BC于E,BD⊥AD.求证:AE=2BD.
如图所示,Rt△ABC中,∠ACB=90°,∠BAC=45°,AD为∠BAC平分线交BC于E,BD⊥AD.求证:AE=2BD.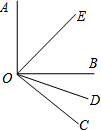 如图所示,OE和OD分别是∠AOB和∠BOC的平分线,且∠AOB=90°.
如图所示,OE和OD分别是∠AOB和∠BOC的平分线,且∠AOB=90°.