题目内容
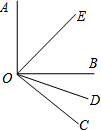 如图所示,OE和OD分别是∠AOB和∠BOC的平分线,且∠AOB=90°.
如图所示,OE和OD分别是∠AOB和∠BOC的平分线,且∠AOB=90°.(1)若∠BOC=40°,求∠EOD的度数;
(2)若∠AOB+∠BOC=x°,直接写出用含x的式子表示∠EOD的度数.
考点:角的计算,角平分线的定义
专题:
分析:(1)根据角平分线定义求出∠BOE=
∠AOB=45°,∠BOD=
∠BOC=20°,代入∠EOD=∠BOE+∠BOD求出即可;
(2)根据角平分线定义求出∠BOE=
∠AOB,∠BOD=
∠BOC,代入∠EOD=∠BOE+∠BOD求出即可.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据角平分线定义求出∠BOE=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵OE和OD分别是∠AOB和∠BOC的平分线,∠AOB=90°,∠BOC=40°,
∴∠BOE=
∠AOB=45°,∠BOD=
∠BOC=20°,
∴∠EOD=∠BOE+∠BOD=45°+20°=65°;
(2)∵OE和OD分别是∠AOB和∠BOC的平分线,∠AOB+∠BOC=x°,
∴∠BOE=
∠AOB,∠BOD=
∠BOC,
∴∠EOD=∠BOE+∠BOD=
(∠AOB+∠BOC)=
x°.
∴∠BOE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EOD=∠BOE+∠BOD=45°+20°=65°;
(2)∵OE和OD分别是∠AOB和∠BOC的平分线,∠AOB+∠BOC=x°,
∴∠BOE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EOD=∠BOE+∠BOD=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了角平分线定义,角的有关计算的应用,解此题的关键是求出∠EOD=
(∠AOB+∠BOC).
| 1 |
| 2 |

练习册系列答案
相关题目
在下列条件中,△ABC不是直角三角形的是( )
| A、b2=a2-c2 |
| B、a2:b2:c2=1:3:2 |
| C、∠C=∠A-∠B |
| D、∠A:∠B:∠C=3:4:5 |
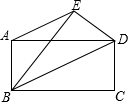 把矩形ABCD沿对角线BD折叠使点C落在点E处,连接AE,得到梯形ABDE,AB=12cm,BC=16cm,求梯形ABDE的面积.
把矩形ABCD沿对角线BD折叠使点C落在点E处,连接AE,得到梯形ABDE,AB=12cm,BC=16cm,求梯形ABDE的面积.