题目内容
 如图,已知PA、PB分别与⊙O相切于点A、B,点C在PB上,且CO∥PA,CD⊥PA于点D.
如图,已知PA、PB分别与⊙O相切于点A、B,点C在PB上,且CO∥PA,CD⊥PA于点D.(1)求证:CO=DA;
(2)若⊙O的半径为6,BC=8,求AD的长.
考点:切线的性质
专题:
分析:(1)连接OA,由切线的性质可知OA⊥AP,再由CD⊥AP可知四边形ANMO是矩形,故可得出结论;
(2)连接OB,则OB⊥BP由OA=MN,OA=OB,CO∥AP.可知OB=CD,∠OCB=∠DPC.故可得出Rt△OCB≌△CPD,OC=CP,PD=BC,在Rt△CDP利用勾股定理即可求PC的值,进而求得AD的长.
(2)连接OB,则OB⊥BP由OA=MN,OA=OB,CO∥AP.可知OB=CD,∠OCB=∠DPC.故可得出Rt△OCB≌△CPD,OC=CP,PD=BC,在Rt△CDP利用勾股定理即可求PC的值,进而求得AD的长.
解答: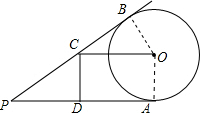 (1)证明:如图,连接OA,则OA⊥AP,
(1)证明:如图,连接OA,则OA⊥AP,
∵CD⊥AP,
∴CD∥OA,
∵CO∥AP,
∴四边形ANMO是矩形,
∴CO=DA;
(2)解:连接OB,则OB⊥BP
∵OA=CD,OA=OB,CO∥AP.
∴OB=CD,∠OCB=∠DPC,
在△OCB和△CPD中,
,
∴△OCB≌△CPD(AAS),
∴OC=CP,PD=BC=8,
在Rt△MNP中,有PC2=CD2+PD2,
即PC2=62+82,
∴PC=10,
∴AD=10.
 (1)证明:如图,连接OA,则OA⊥AP,
(1)证明:如图,连接OA,则OA⊥AP,∵CD⊥AP,
∴CD∥OA,
∵CO∥AP,
∴四边形ANMO是矩形,
∴CO=DA;
(2)解:连接OB,则OB⊥BP
∵OA=CD,OA=OB,CO∥AP.
∴OB=CD,∠OCB=∠DPC,
在△OCB和△CPD中,
|
∴△OCB≌△CPD(AAS),
∴OC=CP,PD=BC=8,
在Rt△MNP中,有PC2=CD2+PD2,
即PC2=62+82,
∴PC=10,
∴AD=10.
点评:本题考查的是切线的性质、全等三角形的判定与性质、勾股定理及矩形的判定与性质,在解答此类题目时往往连接圆心与切点,构造出直角三角形,再根据直角三角形的性质解答.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
圆心在坐标原点,其半径为7的圆,则下列各点在圆外的是( )
| A、(3,4) |
| B、(4,4) |
| C、(4,5) |
| D、(4,6) |
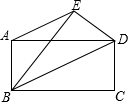 把矩形ABCD沿对角线BD折叠使点C落在点E处,连接AE,得到梯形ABDE,AB=12cm,BC=16cm,求梯形ABDE的面积.
把矩形ABCD沿对角线BD折叠使点C落在点E处,连接AE,得到梯形ABDE,AB=12cm,BC=16cm,求梯形ABDE的面积. 如图,正方形ABCD边长为4,点E在边AB上(点E与点A、B不重合),过点A作AF⊥DE,垂足为G,AF与边BC相交于点F.
如图,正方形ABCD边长为4,点E在边AB上(点E与点A、B不重合),过点A作AF⊥DE,垂足为G,AF与边BC相交于点F.