题目内容
 如图所示,Rt△ABC中,∠ACB=90°,∠BAC=45°,AD为∠BAC平分线交BC于E,BD⊥AD.求证:AE=2BD.
如图所示,Rt△ABC中,∠ACB=90°,∠BAC=45°,AD为∠BAC平分线交BC于E,BD⊥AD.求证:AE=2BD.考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:延长BD和AC交于F,求出∠CAE=∠CBF,AC=BC,证△EAC≌△FBC,△BAD≌△FAD,推出AE=BF,BD=DF,即可得出答案.
解答: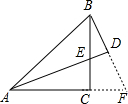 证明:延长BD和AC交于F,
证明:延长BD和AC交于F,
∵Rt△ABC中,∠ACB=90°,∠BAC=45°,
∴∠ABC=45°=∠BAC,
∴AC=BC,
∵∠ACB=90°,
∴∠ACE=∠BCF=90°,
∵AD平分∠BAC,
∴∠BAD=∠EAC,
∵BD⊥AD,
∴∠ACE=BDE=90°,
∵∠AEC=∠BED,
∴根据三角形内角和定理得:∠DBE=∠CAE,
在△ACE和△BCF中,
,
∴△ACE≌△BCF(SAS),
∴AE=BF,
在△BAD和△FAD中,
,
∴△BAD≌△FAD(ASA),
∴BD=DF,
即BF=2BD,
∴AE=2BD.
 证明:延长BD和AC交于F,
证明:延长BD和AC交于F,∵Rt△ABC中,∠ACB=90°,∠BAC=45°,
∴∠ABC=45°=∠BAC,
∴AC=BC,
∵∠ACB=90°,
∴∠ACE=∠BCF=90°,
∵AD平分∠BAC,
∴∠BAD=∠EAC,
∵BD⊥AD,
∴∠ACE=BDE=90°,
∵∠AEC=∠BED,
∴根据三角形内角和定理得:∠DBE=∠CAE,
在△ACE和△BCF中,
|
∴△ACE≌△BCF(SAS),
∴AE=BF,
在△BAD和△FAD中,
|
∴△BAD≌△FAD(ASA),
∴BD=DF,
即BF=2BD,
∴AE=2BD.
点评:本题考查了全等三角形的性质和判定的应用,解此题的关键是求出AE=BF和BD=DF,题目比较好,难度适中.

练习册系列答案
相关题目
 如图所示,△ABC中,已知∠BAC等于45度,AD⊥BC于D,BD等于3,DC等于2,求AD的长.小萍同学灵活运用轴对称知识,将图形进行翻折变换巧妙地解答了此题.
如图所示,△ABC中,已知∠BAC等于45度,AD⊥BC于D,BD等于3,DC等于2,求AD的长.小萍同学灵活运用轴对称知识,将图形进行翻折变换巧妙地解答了此题.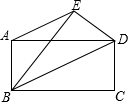 把矩形ABCD沿对角线BD折叠使点C落在点E处,连接AE,得到梯形ABDE,AB=12cm,BC=16cm,求梯形ABDE的面积.
把矩形ABCD沿对角线BD折叠使点C落在点E处,连接AE,得到梯形ABDE,AB=12cm,BC=16cm,求梯形ABDE的面积. 某村在村口建可有个如图所示的牌门,牌门上部是圆弧AD,已知牌门的宽BC为4m,立柱BC,CD高为2m,弧AD的中点E与BC距离为3m.
某村在村口建可有个如图所示的牌门,牌门上部是圆弧AD,已知牌门的宽BC为4m,立柱BC,CD高为2m,弧AD的中点E与BC距离为3m.