题目内容
 如图,在△ABC中,AB=AC,AD⊥BC,CE⊥AB,AD=12,CE=8,求S△ABC.
如图,在△ABC中,AB=AC,AD⊥BC,CE⊥AB,AD=12,CE=8,求S△ABC.考点:勾股定理,等腰三角形的性质
专题:
分析:首先利用三角形面积公式得出AB,BC之间的关系,进而利用勾股定理求出BC的长,进而得出答案.
解答:解: ∵S△ABC=
∵S△ABC=
•BC•AD=
AB•EC,
∴12BC=8AB,
∴AB=
BC,
∵AB=AC,
∴BD=DC=
BC,
∵AD2+BD2=AB2,
∴(
BC)2=122+(
BC)2,
∴BC=6
,
∴S△ABC=
•BC•AD=
×6
×12=36
.
 ∵S△ABC=
∵S△ABC=| 1 |
| 2 |
| 1 |
| 2 |
∴12BC=8AB,
∴AB=
| 3 |
| 2 |
∵AB=AC,
∴BD=DC=
| 1 |
| 2 |
∵AD2+BD2=AB2,
∴(
| 3 |
| 2 |
| 1 |
| 2 |
∴BC=6
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
点评:此题主要考查了勾股定理以及三角形面积公式应用,得出BC的长是解题关键.

练习册系列答案
相关题目
在下列条件中,△ABC不是直角三角形的是( )
| A、b2=a2-c2 |
| B、a2:b2:c2=1:3:2 |
| C、∠C=∠A-∠B |
| D、∠A:∠B:∠C=3:4:5 |
 如图所示,△ABC中,已知∠BAC等于45度,AD⊥BC于D,BD等于3,DC等于2,求AD的长.小萍同学灵活运用轴对称知识,将图形进行翻折变换巧妙地解答了此题.
如图所示,△ABC中,已知∠BAC等于45度,AD⊥BC于D,BD等于3,DC等于2,求AD的长.小萍同学灵活运用轴对称知识,将图形进行翻折变换巧妙地解答了此题.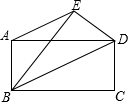 把矩形ABCD沿对角线BD折叠使点C落在点E处,连接AE,得到梯形ABDE,AB=12cm,BC=16cm,求梯形ABDE的面积.
把矩形ABCD沿对角线BD折叠使点C落在点E处,连接AE,得到梯形ABDE,AB=12cm,BC=16cm,求梯形ABDE的面积.