题目内容
17.解下列不等式,并把解集在数轴上表示出来(1)3(x+2)-5x<-3
(2)1-$\frac{x-2}{3}$≥$\frac{x+1}{2}$.
分析 (1)根据不等式基本性质依次:去括号、移项、合并同类项、系数化为1可得解集,再表示在数轴上根据:大于向右,不包括用空心点表示解集即可;
(2)两边都乘以6去分母后,再依次去括号、移项、合并同类项、系数化为1可得解集,再在数轴上根据:小于向左,包括用实心点表示解集即可.
解答 解:(1)去括号,得:3x+6-5x<-3,
移项、合并,得:-2x<-9,
系数化为1,得:x>$\frac{9}{2}$;
将解集表示在数轴上如图:
(2)去分母,得:6-2(x-2)≥3(x+1),
去括号,得:6-2x+4≥3x+3,
移项、合并,得:-5x≥-7,
系数化为1,得:x≤$\frac{7}{5}$.
将解集表示在数轴上如图:
点评 本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.

练习册系列答案
相关题目
7.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (3a)3=9a3 | C. | a3-2a3=-1 | D. | (a2)3=a6 |
12.如果一个多边形的每一个内角都相等,且每一个内角的度数为135°,那么这个多边形的边数为( )
| A. | 6 | B. | 7 | C. | 8 | D. | 以上答案都不对 |
2.设a,b是方程x2+x-2016=0的两个实数根,则a2+2a+b的值为( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
 如图,已知AB∥CD,∠BAE=3∠ECF,∠ECF=28°,求∠E的度数.
如图,已知AB∥CD,∠BAE=3∠ECF,∠ECF=28°,求∠E的度数.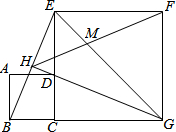 如图,正方形ABCD的边CD在正方形ECGF边CE上,DG平分∠EGC,延长GD交BE于H,EG与FH交于点M,若DC=$2-\sqrt{2}$,则GM=$\sqrt{2}$.
如图,正方形ABCD的边CD在正方形ECGF边CE上,DG平分∠EGC,延长GD交BE于H,EG与FH交于点M,若DC=$2-\sqrt{2}$,则GM=$\sqrt{2}$.