题目内容
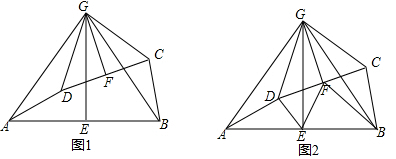
3.如图1,在四边形ABCD中,已知:AD=BC,点E、F分别是AB、CD的中点,AB、CD的垂直平分线交于点G,连接AG、BG、CG、DG.(1)求证:∠AGD=∠BGC;
(2)求证:△AGD∽△EGF;
(3)如图2,连接BF、ED,求证:S△GBF=S△GED.
分析 (1)由GE是AB的垂直平分线,得到GA=GB,同理:GD=GC,根据全等三角形的性质即刻得到结论;
(2)根据相似三角形的性质得到$\frac{EG}{FG}=\frac{GA}{GD}$,根据相似三角形的判定定理即刻得到结论;
(3)根据相似三角形的性质得到$\frac{GB}{GD}=\frac{GE}{GF}$,即 GB•GF=GE•GD,由于S△GBF=$\frac{1}{2}$GB•GF•sin∠BGF,S△GED=$\frac{1}{2}$GE•GD•sin∠EGD,于是得到结论.
解答 解:(1)证明:∵GE是AB的垂直平分线,
∴GA=GB,
同理:GD=GC,
在△AGD和△BGC中,$\left\{{\begin{array}{l}{GA=GB}\\{GD=GC}\\{AD=BC}\end{array}}\right.$,
∴△AGD≌△BGC(SSS),
∴∠AGD=∠BGC;
(2)证明:∵∠AGD=∠BGC,
∴∠AGB=∠DGC,
在△AGB和△DGC中,$\frac{GA}{GD}=\frac{GB}{GC}$,
∴△AGB∽△DGC,$\frac{EG}{FG}=\frac{GA}{GD}$,
又∵∠AGE=∠DGF,
∴∠AGD=∠EGF,
∴△AGD∽△EGF;
(3)∵△GAB∽△GCD,
∴$\frac{GB}{GD}=\frac{GE}{GF}$,即 GB•GF=GE•GD,
∵GE垂直平分AB,
∴AG=BG,
∴∠AGE=∠BGE,
∵∠AGD=∠EGF,
∴∠DGE=∠BGF,
∵S△GBF=$\frac{1}{2}$GB•GF•sin∠BGF,S△GED=$\frac{1}{2}$GE•GD•sin∠EGD,
∴S△GBF=S△GED.
点评 本题考查了全等三角形的判断和性质,相似三角形的判定和性质,三角形的面积的计算,线段垂直平分线的性质,证得△GAB∽△GCD是解题的关键.

 阅读快车系列答案
阅读快车系列答案| 郊县 | 人数/万 | 人均耕地面积/公顷 |
| A | 20 | 0.15 |
| B | 5 | 0.20 |
| C | 10 | 0.18 |
| A. | 胜2局与负3局 | B. | 盈利3万元与亏损3万元 | ||
| C. | 向东走100m与向北走100m | D. | 转盘逆时针转6圈与顺时针转6圈 |

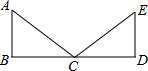 如图,已知AB⊥BD,AB∥ED,AB=ED,要说明△ABC≌△EDC,若以“SAS”为依据,还要添加的条件为BC=CD;若添加条件∠ACB=∠ECD,则可以用AAS公理(或定理)判定全等.
如图,已知AB⊥BD,AB∥ED,AB=ED,要说明△ABC≌△EDC,若以“SAS”为依据,还要添加的条件为BC=CD;若添加条件∠ACB=∠ECD,则可以用AAS公理(或定理)判定全等.