题目内容
8.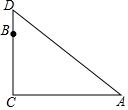 在一棵树的10米高处有两个猴子为抢吃池塘边水果,一只猴子爬下树跑到A处(离树20米)的池塘边.另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高15米.
在一棵树的10米高处有两个猴子为抢吃池塘边水果,一只猴子爬下树跑到A处(离树20米)的池塘边.另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高15米.
分析 由题意知AD+DB=BC+CA,设BD=x,则AD=30-x,且在直角△ACD中CD2+CA2=AD2,代入勾股定理公式中即可求x的值,树高CD=(10+x)米即可.
解答 解:由题意知AD+DB=BC+CA,且CA=20米,BC=10米,
设BD=x,则AD=30-x,
∵在Rt△ACD中:CD2+CA2=AD2,
即(30-x)2=(10+x)2+202,
解得x=5米,故树高为CD=10+x=15米,
答:树高为15米.
故答案为:15.
点评 本题考查了勾股定理在实际生活中的应用,本题中找到AD+DB=BC+CA的等量关系,并根据勾股定理CD2+CA2=AD2求解是解题的关键.

练习册系列答案
相关题目
13.下列式子(1)$\sqrt{6}$,(2)$\sqrt{{a}^{2}+1}$,(3)$\root{3}{9}$,(4)$\sqrt{{a}^{2}+2a+1}$,(5)$\sqrt{|{m}^{2}-1|}$中,是二次根式的是( )
| A. | (1)(2)(3)(4) | B. | (2)(3)(4)(5) | C. | (1)(2)(3)(5) | D. | (1)(2)(4)(5) |
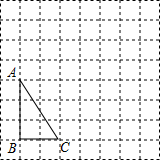 如图,在方格纸上,以格点连线为边的三角形叫做格点三角形,请按要求完成下列操作:先将格点△ABC绕A点逆时针旋转90°得到△A1B1C1,再将△A1B1C1沿直线B1C1作轴对称得到△A2B2C2.
如图,在方格纸上,以格点连线为边的三角形叫做格点三角形,请按要求完成下列操作:先将格点△ABC绕A点逆时针旋转90°得到△A1B1C1,再将△A1B1C1沿直线B1C1作轴对称得到△A2B2C2. 如图,已知线段AB=4cm.
如图,已知线段AB=4cm. 学习完轴对称后,黑板展示区出了一道作图题(不写作法,保留作图痕迹).
学习完轴对称后,黑板展示区出了一道作图题(不写作法,保留作图痕迹).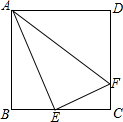 如图,正方形ABCD中,E是BC的中点,F是CD上的一点,且CD=4CF.求证:∠AEF=90°.
如图,正方形ABCD中,E是BC的中点,F是CD上的一点,且CD=4CF.求证:∠AEF=90°. 如图,∠1=47°,∠2=133°,∠D=47°,那么图中哪些线段平行?并说明理由.
如图,∠1=47°,∠2=133°,∠D=47°,那么图中哪些线段平行?并说明理由.