题目内容
18.已知函数y=$k(x-\frac{2}{k})(x+2)(k≠0)$.(1)|k|=2,请画出符合条件的函数图象;
(2)k的值分别取k1,k2时,得到两个函数${y}_{1}{=}_{{k}_{1}}(x-\frac{2}{{k}_{1}})(x+2)$,${y}_{2}{=}_{{k}_{2}}(x-\frac{2}{{k}_{2}})(x+2)$,其中k1<k2且k1+k2=0,y2的图象是由y1的图象经过怎样的变换得到的;
(3)在(2)的条件下,请求出当y1<y2时,x的取值范围.
分析 (1)根据绝对值定义得:k=±2,代入抛物线解析式中画图即可;
(2)根据已知k1<k2且k1+k2=0,得:k2=-k1,分别求出y1和y2的顶点坐标和与x轴的交点坐标,根据|k1|=|k2|可知,y1与y2的开口大小相同,方向相反,可得结论;
(3)由两函数与x轴的交点可知:都过(-2,0),将x=0代入,y=-4,所以过(0,-4),根据(1)问的图象可得结论.
解答 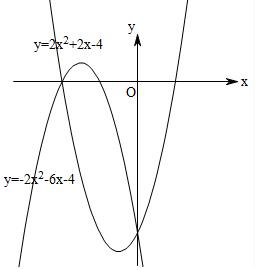 解:(1)∵|k|=2,
解:(1)∵|k|=2,
∴k=2或-2,
∴y=2(x-1)(x+2)=2x2+2x-4或y=-2(x+1)(x+2)=-2x2-6x-4,
图象如右图:
(2)∵k1<k2且k1+k2=0,k1≠0,k2≠0,
∴k2=-k1,
∴k2>0,k1<0,
∴${y}_{2}{=}_{{k}_{2}}(x-\frac{2}{{k}_{2}})(x+2)$=-k1(x+$\frac{2}{{k}_{1}}$)(x+2),
顶点坐标为:(-$\frac{1}{{k}_{1}}$-1,${k}_{1}-2+\frac{1}{{k}_{1}}$),
与x轴交点为:(-$\frac{2}{{k}_{1}}$,0),(-2,0),
由${y}_{1}{=}_{{k}_{1}}(x-\frac{2}{{k}_{1}})(x+2)$知,顶点坐标为:($\frac{1}{{k}_{1}}$-1,-$\frac{1}{{k}_{1}}-2-{k}_{1}$),与x轴交点为:($\frac{2}{{k}_{1}}$,0),(-2,0),
∵|k1|=|k2|,
∴y2的图象可由y1的图象变换得到,
即y1向右平移-$\frac{2}{{k}_{1}}$(因为k1<0,-$\frac{2}{{k}_{1}}$>0)个单位,再向上平移4个单位后,再沿x轴翻折(关于x轴对称)可得y2图象;
(3)当x=0时,y1=-4,y2=-4,
∵y1与y2的交点分别为(-2,0)和(0,-4),
∴当y1<y2时,x<-2或x>0.
点评 本题考查了二次函数的性质和平移变换,有难度,第二问分别求出两函数的顶点坐标是关键,第三问利用数形结合的思想解决问题.

| A. | 134° | B. | 64° | C. | 144° | D. | 54° |
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
| A. | 12cm | B. | 9cm | C. | 7cm | D. | 12cm或9cm |
 如图,射线OA的方向是西南方向,射线OB的方向是北偏西70°,则∠AOB=65°.
如图,射线OA的方向是西南方向,射线OB的方向是北偏西70°,则∠AOB=65°.
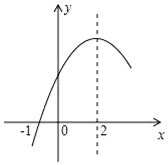 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a-3b+c>0;(3)4a+2b>m(am+b),(m≠2的实数)(4)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论有( )个.
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a-3b+c>0;(3)4a+2b>m(am+b),(m≠2的实数)(4)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论有( )个.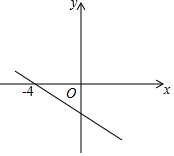 y=-2x-m的图象如图,关于x的不等式-2x-m>0的解集是x<-4.
y=-2x-m的图象如图,关于x的不等式-2x-m>0的解集是x<-4.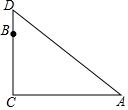 在一棵树的10米高处有两个猴子为抢吃池塘边水果,一只猴子爬下树跑到A处(离树20米)的池塘边.另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高15米.
在一棵树的10米高处有两个猴子为抢吃池塘边水果,一只猴子爬下树跑到A处(离树20米)的池塘边.另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高15米.