题目内容
16．已知a、b为有理数，m、n分别表示5-$\sqrt{7}$的整数部分和小数部分，且am+bn（n+2$\sqrt{7}$）=4，则a+b的值为（ ）| A． | 2 | B． | 1.5 | C． | 1 | D． | 4 |
分析 根据已知首先求出m，n的值，进而化简原式得出2a+2b=4，a+b=2，求出即可．
解答 解：∵m，n分别表示5-$\sqrt{7}$的整数部分和小数部分，
∴m=2，n=5-$\sqrt{7}$-2=3-$\sqrt{7}$，
∴am+bn（n+2$\sqrt{7}$）=2a+b（3$-\sqrt{7}$）（3-$\sqrt{7}$$+2\sqrt{7}$）
=2a+2b=4，
∴a+b=2，
故选A．
点评 本题主要考查了无理数大小的估算和二次根式的混合运算．能够正确估算出一个较复杂的无理数的大小是解决此类问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
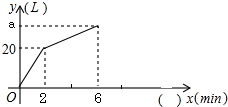一个容器中有一个进水管和两个出水管，从某一时刻开始2min内只进水不出水，在随后的4min内开启了一个出水管，既进水又出水，每个出水管每分钟出水7.5L，每分钟的进水量和出水量保持不变，容器内的水量y（L）与时间x（min）之间的函数关系如图所示．
已知四边形ABCD各顶点的坐标分别是A（0，0），B（3，6），C（6，8），D（8，0）
1．函数y=$\frac{k}{x}$的图象经过点（-2，4），则下列四个点在y=$\frac{k}{x}$图象上的是（ ）
| A． | （4，-2） | B． | （2，4） | C． | （1，8） | D． | （-2，-4） |
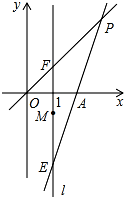如图，在平面直角坐标系中，O为原点，直线l：x=1，点A（2，0），点E，点F，点M都在直线l上，且点E和点F关于点M对称．直线EA与直线OF交于点P．