Question

11．已知四边形ABCD各顶点的坐标分别是A（0，0），B（3，6），C（6，8），D（8，0）
（1）请你借助网格，建立适当的直角坐标系，求出四边形ABCD的面积；
（2）试判断AB、CD是否垂直，并说明理由．

Answer 1

分析 （1）选取适当的点作为坐标原点，经过原点的两条互相垂直的直线分别作为x轴，y轴，建立坐标系，分别描出点A、点B、点C、点D．如确定（3，6）表示的位置，先在x轴上找出表示3的点，再在y轴上找出表示6的点，过这两个点分别做x轴和y轴的垂线，垂线的交点即所要表示的位置．
（2）连接AB与CD并延长解答即可．

解答 解：（1）如图1所示：
四边形ABCD的面积=$8×8-\frac{1}{2}×2×8-\frac{1}{2}×2×3-2×3-\frac{1}{2}×3×6$=38．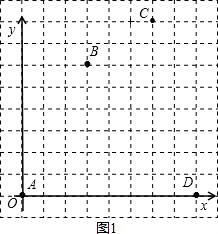
（2）连接AB与CD并延长，如图2：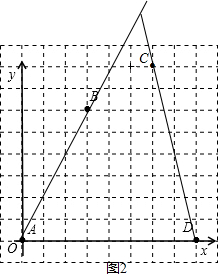

由图可得AB、CD不垂直．

点评 主要考查了直角坐标系的建立．在平面直角坐标系中，一定要理解点与坐标的对应关系，是解决此类问题的关键．