题目内容
4.O为△ABC内一点,BO、CO延长线分别交AC、AB于D、E,如果BE•BA+CD•CA=BC2.求证:A、D、O、E四点共圆.分析 作∠CDF=∠ABC交CB于点F,连接EF,易得△CDF∽△CBA,得出CD•CA=CF•CB=CF•(CF+FB),由BE•BA+CD•CA=BC2,可得出BE•BA=BF•BC,从而得出△BEF∽△BCA,再利用角边关系可得出△CFE∽△DFB,相似三角形的对应角相等,可得∠ADB=∠BEC,从而得出∠ADB+∠AEC=∠BEC+∠AEC=180°,即可得出结论.
解答 解:如图,作∠CDF=∠ABC交CB于点F,连接EF,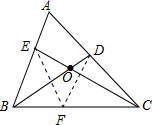
∵∠CDF=∠ABC,∠DCF=∠BCA,
∴△CDF∽△CBA,
∴$\frac{CD}{BC}$=$\frac{CF}{CA}$,即CD•CA=CF•CB=CF•(CF+FB),
∵BE•BA+CD•CA=BC2,
∴BE•BA=BC2-CD•CA=(CF+FB)2-CF•(CF+FB)=FB•(FB+CF)=BF•BC,
∵∠EBF=∠CAB,
∴△BEF∽△BCA,
∴△CDF∽△CBA∽△BEF,
∴$\frac{CF}{DF}$=$\frac{EF}{BF}$,即$\frac{CF}{EF}$=$\frac{DF}{BF}$,
又∵∠EFC=∠EFD+∠DFC=∠EFB+∠DFE=∠DFB.
∴△CFE∽△DFB,
∴∠ADB=∠DCF+∠DBF=∠BEF+∠CEF=∠BEC,
∴∠ADB+∠AEC=∠BEC+∠AEC=180°,
∴A,D,O,E四点共圆.
点评 本题主要考查了四点共圆,涉及相似三角形的判定与性质,四边形共圆的判定,解题的关键是正确作出辅助线,找出相似三角形.

练习册系列答案
相关题目
14.某书店要经营一种新上市的中考数学复习资料,进价为每本20元,试营销阶段发现每天的销售量y(本)与单价x(元/本)之间满足如表:
(1)观察并分析表中的y与x之间的对应关系,用学过的一次函数、反比例函数或二次函数的有关知识写出y(本)与x(元/本)的函数解析式.
(2)写出书店销售这种中考数学复习资料,每天所得的销售利润W(元)与销售单价x(元/本)之间的函数解析式,并求出销售单价为多少时,该书店每天的销售利润最大,最大利润是多少?
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过26元;
方案B:每天销售量不少于50本,且每本资料的利润至少为18元
请比较哪种方案的最大利润更高,并说明理由.
| 销售价格x(元/本) | … | 25 | 30 | 35 | 40 | … |
| 销售量y(本) | … | 250 | 200 | 150 | 100 | … |
(2)写出书店销售这种中考数学复习资料,每天所得的销售利润W(元)与销售单价x(元/本)之间的函数解析式,并求出销售单价为多少时,该书店每天的销售利润最大,最大利润是多少?
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过26元;
方案B:每天销售量不少于50本,且每本资料的利润至少为18元
请比较哪种方案的最大利润更高,并说明理由.
 如图所示,点A,B,C,D,E,F,G,H,K都是8×8方格纸中的格点,为使△DEM∽△ABC,则点M应是F、G、H、K四点中的( )
如图所示,点A,B,C,D,E,F,G,H,K都是8×8方格纸中的格点,为使△DEM∽△ABC,则点M应是F、G、H、K四点中的( )