题目内容
5.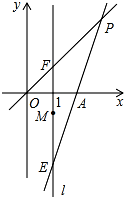 如图,在平面直角坐标系中,O为原点,直线l:x=1,点A(2,0),点E,点F,点M都在直线l上,且点E和点F关于点M对称.直线EA与直线OF交于点P.
如图,在平面直角坐标系中,O为原点,直线l:x=1,点A(2,0),点E,点F,点M都在直线l上,且点E和点F关于点M对称.直线EA与直线OF交于点P.(1)若M点坐标为(1,0)、F点坐标为(1,1),则点E坐标为(1,-1),线段EA=$\sqrt{2}$;
(2)若点M的坐标为(1,-1),当点F的坐标为(1,1)时,如图所示.
①求点P的坐标;
②若在平面直角坐标系中存在点B,使得以B,P,F,E为顶点的四边形为平行四边形,请直接写出点B的坐标.
分析 (1)根据中点性质,可得E点坐标,根据勾股定理,可得EA的长;
(2)①根据待定系数法,可得OF的解析式,EA的解析式,根据解方程组,可得P点坐标;
②根据一组对边平行且相等的四边形是平行四边形,可得答案.
解答 解:(1)由点E和点F关于点M对称,得
E(1,-1),
由勾股定理,得
EA=$\sqrt{(2-1)^{2}+(-1)^{2}}$=$\sqrt{2}$,
故答案为:(1,-1),$\sqrt{2}$;
(2)①∵点O(0,0),F(1,1),
∴直线OF的解析式为y=x.
设直线EA的解析式为:y=kx+b(k≠0),
∵点E和点F关于点M(1,-1)对称,
∴E(1,-3).
又∵A(2,0),点E在直线EA上,
∴$\left\{\begin{array}{l}{2k+b=0}\\{k+b=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=3}\\{b=-6}\end{array}\right.$,
∴直线EA的解析式为:y=3x-6.
∵点P是直线OF与直线EA的交点,则$\left\{\begin{array}{l}{y=x}\\{y=3x-6}\end{array}\right.$,$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$,
∴点P的坐标是(3,3).
②平行四边形EPBF时,点B的坐标是(3,7),
平行四边形EBPF时,B点坐标为(3,-1),
平行四边形EPFB时,B点坐标为(-1,-5),
综上所述:B(3,7),(3,-1),(-1,-5).
点评 本题考查了一次函数综合题,(1)利用了线段中点的性质,勾股定理;(2)利用了待定系数法求函数解析式,解方程组求直线的交点坐标,(3)利用了平行四边形的判定,分类讨论是解题关键.

 智能训练练测考系列答案
智能训练练测考系列答案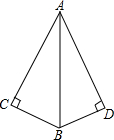 如图所示,∠C=∠D=90°添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.
如图所示,∠C=∠D=90°添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
| A. | AC=AD | B. | AB=AB | C. | ∠ABC=∠ABD | D. | ∠BAC=∠BAD |
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
 如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为10和6时,则阴影部分的面积为15.
如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为10和6时,则阴影部分的面积为15.