题目内容
2．已知抛物线的顶点是（-$\frac{1}{3}$，$\frac{7}{3}$），与y轴交点的纵坐标为2，则它的解析式为（ ）| A． | y=-3x2-2x+2 | B． | y=3x2+2x+2 | C． | y=-3x2+2x-2 | D． | y=-3x2-2x-2 |
分析 根据顶点坐标设抛物线顶点式，将其与y轴交点的坐标代入求得a的值，化简可得．
解答 解：根据题意，设抛物线解析式为y=a（x+$\frac{1}{3}$）2+$\frac{7}{3}$，
将点（0，2）代入，得：$\frac{1}{9}$a+$\frac{7}{3}$=2，
解得：a=-3，
∴y=-3（x+$\frac{1}{3}$）2+$\frac{7}{3}$=-3x2-2x+2，
故选：A．
点评 本题主要考查待定系数法求二次函数解析式，在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．
练习册系列答案
相关题目
如图，已知菱形ABCD的两条对角线长分别是6和8，点M、N分别是边BC、AB上的动点，在对角线AC上找一点P，使PM+PN有最小值，其最小值是$\frac{24}{5}$．
17．化简（$\sqrt{3}$-2）200•（$\sqrt{3}+2$）201的结果为（ ）
| A． | -1 | B． | $\sqrt{3}$-2 | C． | $\sqrt{3}$+2 | D． | -$\sqrt{3}$-2 |
14．下列方程是关于x的一元二次方程的是（ ）
| A． | （x+1）2=x+1 | B． | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$+2=0 | C． | $\sqrt{{x}^{2}-1}$=0 | D． | x2+2x=x2-1 |
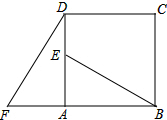如图，四边形ABCD是正方形，△ADF旋转一定角度后得到△ABE，如果AF=4，AB=7．