题目内容
1.已知3k-5x<2,若要使x不为负数,则k的取值范围是k≥$\frac{2}{3}$.分析 先用k表示出不等式的取值范围,再根据x不为负数,求出k的取值范围即可.
解答 解:解不等式3k-5x<2得,x>-$\frac{2}{5}$+$\frac{3}{5}$k,
∵x不为负数,
∴x≥0,即-$\frac{2}{5}$+$\frac{3}{5}$k≥0,解得k≥$\frac{2}{3}$.
故答案为:k≥$\frac{2}{3}$.
点评 本题考查的是解一元一次不等式,熟知不等式的基本性质是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.下列根式中,与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{\frac{3}{2}}$ | C. | $\sqrt{12}$ | D. | $\sqrt{18}$ |
11.某商品连续两次降价10%后的价格是81元,则该商品原来的价格是( )
| A. | 100元 | B. | 90元 | C. | 810元 | D. | 819元 |
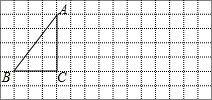 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形.
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形.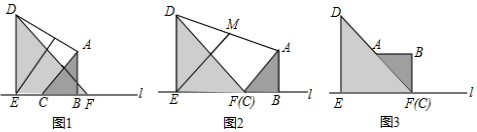
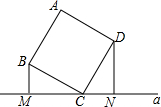 如图,正方形ABCD的顶点C在直线a上,且BM⊥直线a于M,DN⊥直线a于N
如图,正方形ABCD的顶点C在直线a上,且BM⊥直线a于M,DN⊥直线a于N  有“安徽第一楼”之称的安徽省国际金融大厦是具有国际化、专业化、现代化的金融服务场所,它由高度不同的两座楼组成,如图,从左楼丁C处测得右楼楼顶A处的仰角为60°,在左楼楼底D处测得A处的仰角为75°,已知左楼CD高126米,请你利用已知数据估算右楼AB的高.(结果精确到1米,$\sqrt{3}$≈1.7)
有“安徽第一楼”之称的安徽省国际金融大厦是具有国际化、专业化、现代化的金融服务场所,它由高度不同的两座楼组成,如图,从左楼丁C处测得右楼楼顶A处的仰角为60°,在左楼楼底D处测得A处的仰角为75°,已知左楼CD高126米,请你利用已知数据估算右楼AB的高.(结果精确到1米,$\sqrt{3}$≈1.7)