题目内容
13.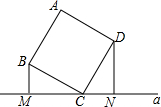 如图,正方形ABCD的顶点C在直线a上,且BM⊥直线a于M,DN⊥直线a于N
如图,正方形ABCD的顶点C在直线a上,且BM⊥直线a于M,DN⊥直线a于N (1)求证:MN=BM+DN;
(2)若点B,D到a的距离分别是1,2.求正方形ABCD的面积.
分析 (1)根据全等三角形的判定定理证得△BMC≌△NCD,得到MC=ND,BM=CN,即可得到结果;
(2)由(1)证得CM=DN=2,根据勾股定理求得BC即可求得结果.
解答 (1)证明:∵∠MBC+∠BCM=∠NCD+∠BCM=90°
∴∠MBC=∠NCD
又∵∠BMC=∠CND=90°,BC=CD
在△BMC与△NCD中,
$\left\{\begin{array}{l}{∠BMC=∠CND}\\{∠MBC=∠NCD}\\{BC=CD}\end{array}\right.$
∴△BMC≌△NCD(AAS),
∴MC=ND,BM=CN,
∴MN=CM+CN=DN+BM;
(2)由(1)证得CM=DN=2,
∴BC=$\sqrt{{1}^{2}{+2}^{2}}$=$\sqrt{5}$,
∴正方形ABCD的面积=BC2=${(\sqrt{5})}^{2}$=5.
点评 本题考查勾股定理、正方形的性质以及三角形全等的判定与性质的应用.在证明三角形的全等时,要注意找准对应角.

练习册系列答案
相关题目
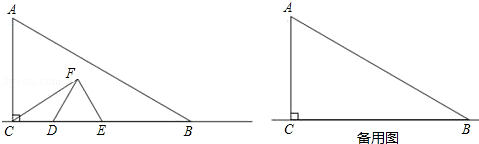
 如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,
如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,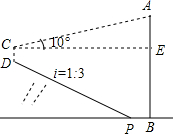 如图,斜坡下一块平地上有一直立的电线杆AB,小华从山坡下点P沿斜坡向上走15.8m到达点D,用高为1.5m的测角仪CD,测得电线杆顶端的仰角为10°,已知斜坡的坡度为i=1:3,山坡下点P到电线杆的距离PB为6m,求电线杆AB的高.(已知sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,$\sqrt{10}$≈3.16,精确到0.1m)
如图,斜坡下一块平地上有一直立的电线杆AB,小华从山坡下点P沿斜坡向上走15.8m到达点D,用高为1.5m的测角仪CD,测得电线杆顶端的仰角为10°,已知斜坡的坡度为i=1:3,山坡下点P到电线杆的距离PB为6m,求电线杆AB的高.(已知sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,$\sqrt{10}$≈3.16,精确到0.1m)