题目内容
14.如图1,正方形ABCD顶点A、B在函数y=$\frac{k}{x}$(k>0)的图象上,点C、D分别在x轴、y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.(1)若点A的横坐标为3,求点D的纵坐标;
(2)如图2,当k=8时,分别求出正方形A′B′C′D′的顶点A′、B′两点的坐标;
(3)当变化的正方形ABCD与(2)中的正方形A′B′C′D′有重叠部分时,求k的取值范围.
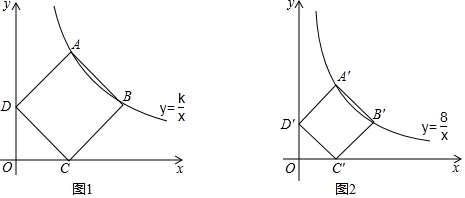
分析 (1)过点A作AE⊥y轴于点E,如图1,则∠AED=90°.利用正方形的性质得AD=DC,∠ADC=90°,再根据等角的余角相等得到∠EDA=∠OCD,则利用“AAS”可判断△AED≌△DOC,从而得到OD=EA=3,于是确定点D的纵坐标为3;
(2)作A′M⊥y轴于M,B′N⊥x轴于点N,如图2,设OD′=a,OC′=b,同理可得△B′C′N≌△C′D′O≌△A′D′E,利用全等的性质得C′N=OD′=A′M=a,B′N=C′O=D′M=b,则A′(a,a+b),B′(a+b,b),再根据反比例函数图象上点的坐标特征得到a(a+b)=8,b(a+b)=8,解方程组求出a、b,从而得到A′、B′两点的坐标;
(3)先利用待定系数法求出直线A′B′解析式为y=-x+6,直线C′D′解析式为y=-x+2,设点A的坐标为(m,2m),则点D坐标为(0,m),若当A点在直线C′D′上时,则2m=-m+2,解得m=$\frac{2}{3}$,可确定此时点A的坐标,从而得到此时k的值;当点D在直线A′B′上时,则m=6,同样可确定此时点A的坐标和k的值,所以可确定当变化的正方形ABCD与(2)中的正方形A′B′C′D′有重叠部分时k的取值范围.
解答 解:(1)过点A作AE⊥y轴于点E,如图1,则∠AED=90°.
∵四边形ABCD为正方形,
∴AD=DC,∠ADC=90°,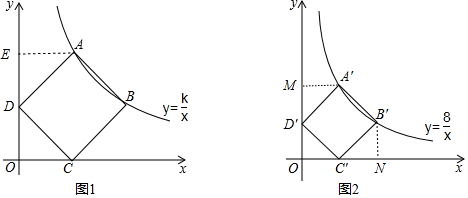
∴∠ODC+∠EDA=90°.
∵∠ODC+∠OCD=90°,
∴∠EDA=∠OCD,
在△AED和△DOC中
$\left\{\begin{array}{l}{∠AED=∠DOC}\\{∠EDA=∠OCD}\\{AD=DC}\end{array}\right.$,
∴△AED≌△DOC(AAS),
∴OD=EA=3,
∴点D的纵坐标为3;
(2)作A′M⊥y轴于M,B′N⊥x轴于点N,如图2,设OD′=a,OC′=b,
同理可得△B′C′N≌△C′D′O≌△A′D′E,
∴C′N=OD′=A′M=a,B′N=C′O=D′M=b,
∴A′(a,a+b),B′(a+b,b),
∵点A′、B′在反比例函数y=$\frac{8}{x}$的图象上,
∴a(a+b)=8,b(a+b)=8,解得a=b=2或a=b=-2(舍去).
∴A′、B′两点的坐标分别为(2,4),(4,2);
(3)设直线A′B′的解析式为y=mx+n,
把A′(2,4),B′(4,2)代入得$\left\{\begin{array}{l}{2m+n=4}\\{4m+n=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-1}\\{n=6}\end{array}\right.$,
∴直线A′B′解析式为y=-x+6,
同样可求得直线C′D′解析式为y=-x+2,
由(2)可知△OCD是等腰直角三角形,
设点A的坐标为(m,2m),点D坐标为(0,m).
当A点在直线C′D′上时,则2m=-m+2,解得m=$\frac{2}{3}$,此时点A的坐标为($\frac{2}{3}$,$\frac{4}{3}$),k=$\frac{2}{3}$×$\frac{4}{3}$=$\frac{8}{9}$;
当点D在直线A′B′上时,有m=6,此时点A的坐标为(6,12),k=6×12=72;
综上可知:当变化的正方形ABCD与(2)中的正方形A′B′C′D′有重叠部分时,k的取值范围为$\frac{8}{9}$≤x≤72.
点评 本题考查了反比例函数的综合题:熟练掌握反比例函数图象上点的坐标特征和正方形的性质;灵活运用全等三角形的性质解决线段相等的问题;会运用待定系数法求一次函数解析式;理解坐标与图形性质.

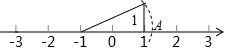 如图,在数轴上点A表示的数为a,则a的值为( )
如图,在数轴上点A表示的数为a,则a的值为( )| A. | $\sqrt{5}$ | B. | -$\sqrt{5}$ | C. | 1-$\sqrt{5}$ | D. | -1+$\sqrt{5}$ |
| A. | 同位角相等 | |
| B. | 有且只有一条直线与已知直线垂直 | |
| C. | 垂线段最短 | |
| D. | 直线外一点到这条直线的垂线段,叫做点到直线的距离 |
 在平面直角坐标系xOy中,已知点A(0,3)、点B(3,0),一次函数y=2x的图象与直线AB交于点M.
在平面直角坐标系xOy中,已知点A(0,3)、点B(3,0),一次函数y=2x的图象与直线AB交于点M. 如图,点B在AD的延长线上,DE∥AC,若∠C=50°,∠BDE=60°,则∠CDB=110°.
如图,点B在AD的延长线上,DE∥AC,若∠C=50°,∠BDE=60°,则∠CDB=110°.
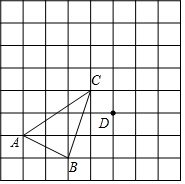 在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移后得△DEF,使点A的对应点为点D,点B的对应点为点E.
在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移后得△DEF,使点A的对应点为点D,点B的对应点为点E.