题目内容
4.在平面直角坐标系中,已知点A(1,3),B(2,-1),C(4,1),点D是该平面内y轴右侧的动点,若以点A、B、C、D为顶点的四边形恰好是平行四边形时,点D的坐标为(5,-3)或(3,5).分析 分三种情况:①BC为对角线时,②AB为对角线时,③AC为对角线时;由平行四边形的性质容易得出点D的坐标.
解答 解:分三种情况:①BC为对角线时,点D的坐标为(5,-3)
②AB为对角线时,点D的坐标为(-1,1),因为点D是该平面内y轴右侧的动点,所以不合题意舍弃
③AC为对角线时,点D的坐标为(3,5)
综上所述,点D的坐标可能是(5,-3)或(3,5);
故答案为:(5,-3)或(3,5).
点评 本题考查了平行四边形的性质、坐标与图形的性质;熟练掌握平行四边形的性质是解决问题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
14.已知二次函数y=ax2-bx+0.5b-a与x轴交于A、B两点,则线段AB的最小值为( )
| A. | 0.5 | B. | 2 | C. | $\sqrt{3}$ | D. | 无法确定 |
19.下列计算正确的是( )
| A. | $\sqrt{3}$+$\sqrt{5}$=$\sqrt{8}$ | B. | $\sqrt{8}$-$\sqrt{3}$=$\sqrt{8-3}$ | C. | $\sqrt{3\frac{2}{3}}$=3$\sqrt{\frac{2}{3}}$ | D. | $\frac{\sqrt{2}}{\sqrt{5}}$=$\frac{\sqrt{10}}{5}$ |
16.已知点A(-1,-5)和点B(2,m),且AB平行于x轴,则B点坐标为( )
| A. | (2,-5) | B. | (2,5) | C. | (2,1) | D. | (2,-1) |
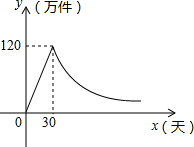 如图,某种商品上市之初采用了大量的广告宣传,其销售量与上市的天数之间成正比,当广告停止后,销售量与上市的天数之间成反比(如图所示),现己知上市30天时,当日销售量为120万件.
如图,某种商品上市之初采用了大量的广告宣传,其销售量与上市的天数之间成正比,当广告停止后,销售量与上市的天数之间成反比(如图所示),现己知上市30天时,当日销售量为120万件. 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.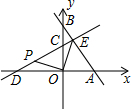 如图,在平面直角坐标系xOy中,直线y=-$\frac{4}{3}$x+4分别与x轴、y轴交于A、B两点,直线y=kx+3分别与x轴、y轴交于D、C两点,且CD=AB.
如图,在平面直角坐标系xOy中,直线y=-$\frac{4}{3}$x+4分别与x轴、y轴交于A、B两点,直线y=kx+3分别与x轴、y轴交于D、C两点,且CD=AB.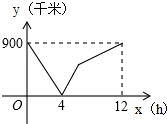 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x小时,两车之间的距离y千米,图中的折线表示y与x之间的函数关系,则出发6小时的时候,甲、乙两车相距450千米.
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x小时,两车之间的距离y千米,图中的折线表示y与x之间的函数关系,则出发6小时的时候,甲、乙两车相距450千米.