题目内容
20.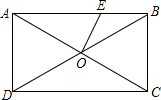 如图,矩形ABCD中,AC交BD于点O,∠AOD=60°,OE⊥AC.若AD=$\sqrt{3}$,则OE=( )
如图,矩形ABCD中,AC交BD于点O,∠AOD=60°,OE⊥AC.若AD=$\sqrt{3}$,则OE=( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 先根据等边三角形的性质得出OA=$\sqrt{3}$,根据△OAE是一个含30°的直角三角形,进而得出OE的长度.
解答 解:∵四边形ABCD是矩形,∠AOD=60°,
∴△ADO是等边三角形,
∴OA=$\sqrt{3}$,∠OAD=60°,
∴∠OAE=30°,
∵OE⊥AC,
∴△OAE是一个含30°的直角三角形,
∴OE=1,
故选A
点评 此题考查矩形的性质,关键是根据等边三角形和直角三角形的性质解答.

练习册系列答案
相关题目
9.下列命题错误的是( )
| A. | 角平分线上的点到角的两边的距离相等 | |
| B. | 圆的切线垂直于过切点的直径 | |
| C. | 多边形外角和等于360° | |
| D. | 相似图形一定是位似图形 |
10.已知直线y=x-3与函数y=$\frac{2}{x}$的图象相交于点(a,b),则a2+b2的值是( )
| A. | 13 | B. | 11 | C. | 7 | D. | 5 |
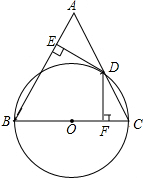 如图,在△ABC中,AB=BC,以BC为直径的⊙O交AC于点D,过点D作DE⊥AB,DF⊥BC,垂足分别为E、F.
如图,在△ABC中,AB=BC,以BC为直径的⊙O交AC于点D,过点D作DE⊥AB,DF⊥BC,垂足分别为E、F.
 已知:如图,∠1=∠2,∠E=∠F,则AB∥CD吗?说明理由.
已知:如图,∠1=∠2,∠E=∠F,则AB∥CD吗?说明理由.