题目内容
8. 已知:如图,∠1=∠2,∠E=∠F,则AB∥CD吗?说明理由.
已知:如图,∠1=∠2,∠E=∠F,则AB∥CD吗?说明理由.
分析 根据平行线的判定推出AE∥DF,根据平行线的性质得出∠EAD=∠FDA,求出∠CDA=∠BAD,根据平行线的判定推出即可.
解答 解:AB∥CD,
理由:∵∠E=∠F,
∴AE∥DF,
∴∠EAD=∠FDA,
∵∠1=∠2,
∴∠1+∠EAD=∠2+∠FDA,
∴∠CDA=∠BAD,
∴AB∥CD.
点评 本题考查了平行线的性质和判定的应用,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
3. 如图,已知AB∥CD,BE平分∠ABC,且交CD于点D,∠CDE=150°,则∠C为( )
如图,已知AB∥CD,BE平分∠ABC,且交CD于点D,∠CDE=150°,则∠C为( )
 如图,已知AB∥CD,BE平分∠ABC,且交CD于点D,∠CDE=150°,则∠C为( )
如图,已知AB∥CD,BE平分∠ABC,且交CD于点D,∠CDE=150°,则∠C为( )| A. | 120° | B. | 150° | C. | 135° | D. | 110° |
13.已知一个平行四边形的一条对角线将其分为两个全等的等腰直角三角形,且这条对角线长为6cm,则另一条对角线长( )cm.
| A. | 6$\sqrt{5}$ | B. | 8 | C. | 6$\sqrt{5}$或8 | D. | 6或6$\sqrt{5}$ |
20.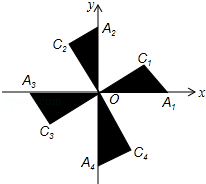 如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2015的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2015的纵坐标为( )
 如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2015的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2015的纵坐标为( )| A. | 0 | B. | -3×($\frac{3\sqrt{3}}{2}$)2013 | C. | (2$\sqrt{3}$)2014 | D. | 3×($\frac{2\sqrt{3}}{3}$)2013 |
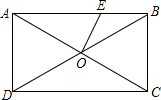 如图,矩形ABCD中,AC交BD于点O,∠AOD=60°,OE⊥AC.若AD=$\sqrt{3}$,则OE=( )
如图,矩形ABCD中,AC交BD于点O,∠AOD=60°,OE⊥AC.若AD=$\sqrt{3}$,则OE=( )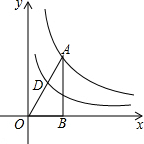 如图,反比例函数y=$\frac{2}{x}$的图象经过△ABO的顶点A,点D是OA的中点,若反比例函数y=$\frac{k}{x}$的图象经过点D,则k的值为$\frac{1}{2}$.
如图,反比例函数y=$\frac{2}{x}$的图象经过△ABO的顶点A,点D是OA的中点,若反比例函数y=$\frac{k}{x}$的图象经过点D,则k的值为$\frac{1}{2}$.