题目内容
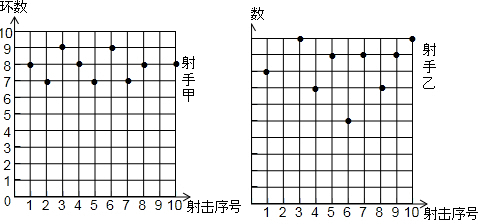
7.甲、乙两名射手在相同条件下打靶,射中的环数如图所示,利用图中提供的信息,解答下列问题:(1)分别求甲、乙两名射手中环数的众数和平均数;
(2)如果从甲、乙两名射手中选一名去参加射击比赛,你选谁去?为什么?
分析 (1)分别根据众数的定义与平均数公式计算即可;
(2)分别计算甲、乙两名射手的方差,然后根据方差小的数据的比较稳定即可选出哪个选手去参加比赛.
解答 解:(1)甲射手所中环数为:8,7,9,8,7,9,7,8,8.出现次数最多的是8,所以甲射手所中环数的众数为8;
乙射手所中环数为:8,10,7,9,5,9,7,9,10.出现次数最多的是9,所以乙射手所中环数的众数为:9;
$\overline{{x}_{甲}}$=$\frac{1}{9}$×(7×3+8×4+9×2)=$\frac{71}{9}$;
$\overline{{x}_{乙}}$=$\frac{1}{9}$×(5+7×2+8+9×3+10×2)=$\frac{74}{9}$;
(2)S甲2=$\frac{1}{9}$[3×(7-$\frac{71}{9}$)2+4×(8-$\frac{71}{9}$)2+2×(9-$\frac{71}{9}$)2]=$\frac{396}{729}$;
S乙2=$\frac{1}{9}$×[(5-$\frac{74}{9}$)2+2×(7-$\frac{74}{9}$)2+(8-$\frac{74}{9}$)2+3×(9-$\frac{74}{9}$)2+2×(10-$\frac{74}{9}$)2]=$\frac{1746}{729}$.
∵S甲2>S乙2,
∴成绩最稳定的选手是乙.
∴如果从甲、乙两名射手中选一名去参加射击比赛,选乙去.
点评 此题主要考查利用方差来判定数据的波动性,方差越小,数据越稳定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列四个数中,比0大的是( )
| A. | -$\frac{2}{3}$ | B. | -$\sqrt{3}$ | C. | 0 | D. | |-2| |
12.为了解决某小区居民的用电情况,一名同学随机抽查了15户家庭的日用电量,结果如下表
则关于这15户家庭的日用电量,下列说法错误的是( )
| 日用电量(单位:度) | 5 | 6 | 7 | 8 | 10 |
| 户数 | 2 | 5 | 4 | 3 | 1 |
| A. | 众数是6度 | B. | 平均数是6.8度 | C. | 中位数是6度 | D. | 极差是5度 |
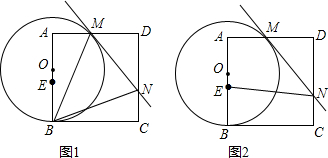
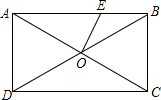 如图,矩形ABCD中,AC交BD于点O,∠AOD=60°,OE⊥AC.若AD=$\sqrt{3}$,则OE=( )
如图,矩形ABCD中,AC交BD于点O,∠AOD=60°,OE⊥AC.若AD=$\sqrt{3}$,则OE=( )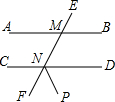 如图,直线AB∥CD,直线EF分别交直线AB、CD于点M、N,NP平分∠DNF,已知∠DNP=55°,则∠EMB=70°.
如图,直线AB∥CD,直线EF分别交直线AB、CD于点M、N,NP平分∠DNF,已知∠DNP=55°,则∠EMB=70°.