题目内容
10.已知直线y=x-3与函数y=$\frac{2}{x}$的图象相交于点(a,b),则a2+b2的值是( )| A. | 13 | B. | 11 | C. | 7 | D. | 5 |
分析 利用反比例函数与一次函数的交点问题得到b=a-3,b=$\frac{2}{a}$,则a-b=3,ab=2,再利用完全平方公式变形得到a2+b2=(a-b)2+2ab,然后利用整体代入的方法计算即可.
解答 解:根据题意得b=a-3,b=$\frac{2}{a}$,
所以a-b=3,ab=2,
所以a2+b2=(a-b)2+2ab=32+2×2=13.
故选A.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了观察函数图象的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4. 如图所示的三角形数垒,a、b是某行的前两个数,当a=7时,b=( )
如图所示的三角形数垒,a、b是某行的前两个数,当a=7时,b=( )
 如图所示的三角形数垒,a、b是某行的前两个数,当a=7时,b=( )
如图所示的三角形数垒,a、b是某行的前两个数,当a=7时,b=( )| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
15.下列四个数中,比0大的是( )
| A. | -$\frac{2}{3}$ | B. | -$\sqrt{3}$ | C. | 0 | D. | |-2| |
20.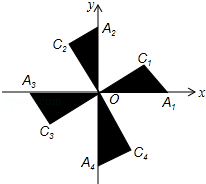 如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2015的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2015的纵坐标为( )
 如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2015的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依此规律,点A2015的纵坐标为( )| A. | 0 | B. | -3×($\frac{3\sqrt{3}}{2}$)2013 | C. | (2$\sqrt{3}$)2014 | D. | 3×($\frac{2\sqrt{3}}{3}$)2013 |
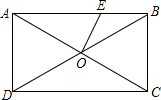 如图,矩形ABCD中,AC交BD于点O,∠AOD=60°,OE⊥AC.若AD=$\sqrt{3}$,则OE=( )
如图,矩形ABCD中,AC交BD于点O,∠AOD=60°,OE⊥AC.若AD=$\sqrt{3}$,则OE=( )
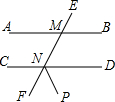 如图,直线AB∥CD,直线EF分别交直线AB、CD于点M、N,NP平分∠DNF,已知∠DNP=55°,则∠EMB=70°.
如图,直线AB∥CD,直线EF分别交直线AB、CD于点M、N,NP平分∠DNF,已知∠DNP=55°,则∠EMB=70°.