题目内容
3.计算:(1)计算:|1-tan60°|-$\frac{6}{\sqrt{3}}$+($\sqrt{2}$-1)0
(2)化简:($\frac{{m}^{2}-1}{{m}^{2}-2m+1}$+$\frac{m}{{m}^{2}-m}$)÷(1+$\frac{2}{m}$)
分析 (1)原式第一项利用绝对值的代数意义化简,第二项分母有理化,最后一项利用零指数幂法则计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=$\sqrt{3}$-1-2$\sqrt{3}$+1=-$\sqrt{3}$;
(2)原式=[$\frac{(m+1)(m-1)}{(m-1)^{2}}$+$\frac{m}{m(m-1)}$]•$\frac{m}{m+2}$=$\frac{m+2}{m-1}$•$\frac{m}{m+2}$=$\frac{m}{m-1}$.
点评 此题考查了分式的混合运算,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列事件中是随机事件的是( )
| A. | 一星期有7天 | |
| B. | 袋中有三个红球,摸出一个球是红球 | |
| C. | 字母M、N都轴对称图形 | |
| D. | 任意买一张车票,座位刚好靠窗口 |
15.下列四个数中,比0大的是( )
| A. | -$\frac{2}{3}$ | B. | -$\sqrt{3}$ | C. | 0 | D. | |-2| |
12.为了解决某小区居民的用电情况,一名同学随机抽查了15户家庭的日用电量,结果如下表
则关于这15户家庭的日用电量,下列说法错误的是( )
| 日用电量(单位:度) | 5 | 6 | 7 | 8 | 10 |
| 户数 | 2 | 5 | 4 | 3 | 1 |
| A. | 众数是6度 | B. | 平均数是6.8度 | C. | 中位数是6度 | D. | 极差是5度 |
13.已知一个平行四边形的一条对角线将其分为两个全等的等腰直角三角形,且这条对角线长为6cm,则另一条对角线长( )cm.
| A. | 6$\sqrt{5}$ | B. | 8 | C. | 6$\sqrt{5}$或8 | D. | 6或6$\sqrt{5}$ |
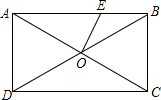 如图,矩形ABCD中,AC交BD于点O,∠AOD=60°,OE⊥AC.若AD=$\sqrt{3}$,则OE=( )
如图,矩形ABCD中,AC交BD于点O,∠AOD=60°,OE⊥AC.若AD=$\sqrt{3}$,则OE=( )