题目内容
15.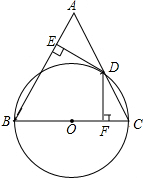 如图,在△ABC中,AB=BC,以BC为直径的⊙O交AC于点D,过点D作DE⊥AB,DF⊥BC,垂足分别为E、F.
如图,在△ABC中,AB=BC,以BC为直径的⊙O交AC于点D,过点D作DE⊥AB,DF⊥BC,垂足分别为E、F.(1)求证:ED是⊙O的切线;
(2)若DF=3$\sqrt{5}$,cosA=$\frac{2}{3}$,求⊙O的直径.
分析 (1)连结OD、BD,先根据圆周角定理得到∠BDC=90°,再根据等腰三角形的性质得到AD=CD,则可判断OD为△ABC的中位线,所以OD∥AB,加上DE⊥AB,则DE⊥OD,然后根据切线的判定定理得ED是⊙O的切线;
(2)根据等腰三角形的性质由AB=AC得到∠A=∠C,在Rt△CFD中利用余弦定理得到cosC=$\frac{CF}{CD}$=cosA=$\frac{2}{3}$,则可设CF=2x,CD=3x,利用勾股定理得到DF=$\sqrt{5}$x,所以$\sqrt{5}$x=3$\sqrt{5}$,解得x=3,于是计算出CD=9,然后在Rt△BCD中利用余弦的定义计算出BC的长即可.
解答 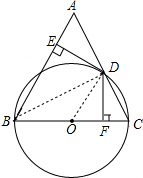 (1)证明:连结OD、BD,
(1)证明:连结OD、BD,
∵BC为直径,
∴∠BDC=90°,
∴BD⊥AC,
而BA=BC,
∴AD=CD,
而OB=OC,
∴OD为△ABC的中位线,
∴OD∥AB,
∵DE⊥AB,
∴DE⊥OD,
∴ED是⊙O的切线;
(2)解:∵AB=AC,
∴∠A=∠C,
在Rt△CFD中,cosC=$\frac{CF}{CD}$=cosA=$\frac{2}{3}$,
设CF=2x,CD=3x,
∴DF=$\sqrt{(3x)^{2}-(2x)^{2}}$=$\sqrt{5}$x,
∴$\sqrt{5}$x=3$\sqrt{5}$,解得x=3,
∴CD=9,
在Rt△BCD中,∵cosC=$\frac{CD}{BC}$=$\frac{2}{3}$,
∴BC=$\frac{3}{2}$×9=$\frac{27}{2}$,
即⊙O的直径为$\frac{27}{2}$.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了解直角三角形.

 阅读快车系列答案
阅读快车系列答案 如图所示的三角形数垒,a、b是某行的前两个数,当a=7时,b=( )
如图所示的三角形数垒,a、b是某行的前两个数,当a=7时,b=( )| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
 如图,已知AB∥CD,BE平分∠ABC,且交CD于点D,∠CDE=150°,则∠C为( )
如图,已知AB∥CD,BE平分∠ABC,且交CD于点D,∠CDE=150°,则∠C为( )| A. | 120° | B. | 150° | C. | 135° | D. | 110° |
 如图,已知△ABC.
如图,已知△ABC. 如图,AB∥CD,点E在BC上,CD=CE,若∠ABC=34°,则∠D的度数是73°.
如图,AB∥CD,点E在BC上,CD=CE,若∠ABC=34°,则∠D的度数是73°.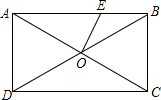 如图,矩形ABCD中,AC交BD于点O,∠AOD=60°,OE⊥AC.若AD=$\sqrt{3}$,则OE=( )
如图,矩形ABCD中,AC交BD于点O,∠AOD=60°,OE⊥AC.若AD=$\sqrt{3}$,则OE=( )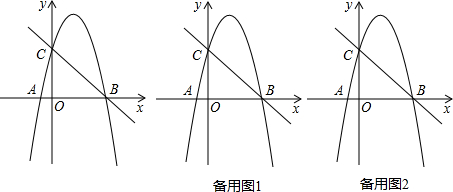
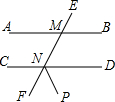 如图,直线AB∥CD,直线EF分别交直线AB、CD于点M、N,NP平分∠DNF,已知∠DNP=55°,则∠EMB=70°.
如图,直线AB∥CD,直线EF分别交直线AB、CD于点M、N,NP平分∠DNF,已知∠DNP=55°,则∠EMB=70°.