题目内容
19.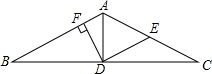 如图,在△ABC中,AB=AC,AD是△ABC点的中线,E是AC的中点,连接AC,DF⊥AB于F.求证:∠BDF=∠ADE.
如图,在△ABC中,AB=AC,AD是△ABC点的中线,E是AC的中点,连接AC,DF⊥AB于F.求证:∠BDF=∠ADE.
分析 根据等腰三角形的性质得到∠BAD=∠CAD,∠ADB=∠ADC=90°,根据等腰三角形的判定定理得到∠CAD=∠ADE.根据余角的性质得到∠BAD=∠BDF,等量代换即可得到结论.
解答 证明:∵AB=AC,AD是△ABC的中线,
∴∠BAD=∠CAD,∠ADB=∠ADC=90°,
∵E是AC的中点,
∴DE=AE=EC,
∴∠CAD=∠ADE.
在Rt△ABD中,∠ADB=90°,
∴∠B+∠BAD=90°.
∵DF⊥AB,
∴∠B+∠BDF=90°,
∴∠BAD=∠BDF,
∴∠BDF=∠CAD,
∴∠BDF=∠ADE.
点评 本题考查了等腰直角三角形的性质,余角的性质,熟练掌握等腰三角形的性质是解题的关键.

练习册系列答案
相关题目
12. 为了了解某中学初中二年级150名男学生的身体发育情况,从中对20名男学生的身高进行了测量,结果如下:(单位:厘米)
为了了解某中学初中二年级150名男学生的身体发育情况,从中对20名男学生的身高进行了测量,结果如下:(单位:厘米)
175 161 171 176 167 181 161 173 171 177 179 172 165 157 173 173 166 177 169 181
如表是根据上述数据填写的频率分布表的一部分:
(1)请填写表中未完成的部分;
(2)样本数据中,男生身高的中位数是172.5厘米;
(3)该校初中二年级男学生身高在171.5---176.5(厘米)范围内的人数为45人;请在右面的坐标系用频数分布直方图的形式将此范围内的学生人数表示出来.
 为了了解某中学初中二年级150名男学生的身体发育情况,从中对20名男学生的身高进行了测量,结果如下:(单位:厘米)
为了了解某中学初中二年级150名男学生的身体发育情况,从中对20名男学生的身高进行了测量,结果如下:(单位:厘米)175 161 171 176 167 181 161 173 171 177 179 172 165 157 173 173 166 177 169 181
如表是根据上述数据填写的频率分布表的一部分:
(1)请填写表中未完成的部分;
(2)样本数据中,男生身高的中位数是172.5厘米;
(3)该校初中二年级男学生身高在171.5---176.5(厘米)范围内的人数为45人;请在右面的坐标系用频数分布直方图的形式将此范围内的学生人数表示出来.
| 分组 | 频数 | 频率 |
| 156.5~161.5 | 3 | 0.15 |
| 161.5~166.5 | 2 | 0.10 |
| 166.5~171.5 | 4 | |
| 171.5~176.5 | 0.30 | |
| 176.5~181.5 | ||
| 合计 | 20 | 1.00 |
8. 如图,平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=155°,则∠A的度数为( )
如图,平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=155°,则∠A的度数为( )
 如图,平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=155°,则∠A的度数为( )
如图,平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=155°,则∠A的度数为( )| A. | 155° | B. | 130° | C. | 125° | D. | 110° |

 如图,在△ABC中,∠BAC=90°,∠C=30°,AE为BC边上的中线.求证:△ABE是等边三角形.
如图,在△ABC中,∠BAC=90°,∠C=30°,AE为BC边上的中线.求证:△ABE是等边三角形. 在正方形网格中,每个小正方形的顶点称为格点,过格点E在四边形ABCD内作矩形EFGH,使得F、G、H分别落在边BC、CD、DA上.
在正方形网格中,每个小正方形的顶点称为格点,过格点E在四边形ABCD内作矩形EFGH,使得F、G、H分别落在边BC、CD、DA上. 如图,已知△ABC,用尺规作出△ABC重心.(保留作图痕迹,不写作法)
如图,已知△ABC,用尺规作出△ABC重心.(保留作图痕迹,不写作法)