题目内容
14.如图1,△ABC内接于⊙O,∠BAC的平分线AD交⊙O于点D,交BC于点E,过点D作DF∥BC,交AB的延长线于点F.(1)求证:△BDE∽∠ADB;
(2)试判断直线DF与⊙O的位置关系,并说明理由;
(3)如图2,条件不变,若BC恰好是⊙O的直径,且AB=6,AC=8,求DF的长.

分析 (1)由AD平分∠BAC,易得∠BAD=∠CAD=∠CBD,又由∠BDE是公共角,即可证得:△BDE∽∠ADB;
(2)首先连接OD,由AD平分∠BAC,可得$\widehat{BD}$=$\widehat{CD}$,由垂径定理,即可判定OD⊥BC,又由BC∥DF,证得结论;
(3)首先过点B作BH⊥AD于点H,连接OD,易证得△BDH∽△BCA,然后由相似三角形的对应边成比例,求得BH的长,继而求得AD的长,然后证得△FDB∽△FAD,又由相似的性质,求得答案.
解答 (1)证明:∵AD平分∠BAC,
∴∠BAD=∠DAC,
∵∠DAC=∠DBC,
∴∠DBC=∠BAD,
∵∠BDE=∠ADB,
∴△BDE∽∠ADB; (2)相切.
(2)相切.
理由:如图1,连接OD,
∵∠BAD=∠DAC,
∴$\widehat{BD}$=$\widehat{CD}$,
∴OD⊥BC,
∵DF∥BC,
∴OD⊥DF,
∴DF与⊙O相切;
(3)如图2,过点B作BH⊥AD于点H,连接OD,
则∠BHD=90°,
∵BC是直径,
∴∠BAC=90°,
∴∠BHD=∠BAC,
∵∠BDH=∠C,
∴△BDH∽△BCA,
∴$\frac{BH}{BA}$=$\frac{BD}{BC}$,
∵AB=6,AC=8,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=10,
∴OB=OD=5,
∴BD=$\sqrt{O{B}^{2}+O{D}^{2}}$=5$\sqrt{2}$,
∴$\frac{BH}{6}$=$\frac{5\sqrt{2}}{10}$,
∴BH=3$\sqrt{2}$,
∴DH=$\sqrt{B{D}^{2}-B{H}^{2}}$=4$\sqrt{2}$,AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=3$\sqrt{2}$,
∴AD=AH+DH=7$\sqrt{2}$,
∵DF与⊙O相切,
∴∠FDB=∠FAD,
∵∠F=∠F,
∴△FDB∽△FAD,
∴$\frac{DF}{AF}$=$\frac{BF}{DF}$=$\frac{BD}{AD}$=$\frac{5\sqrt{2}}{7\sqrt{2}}$,
∴AF=$\frac{7}{5}$DF,BF=$\frac{5}{7}$DF,
∴AB=AF-BF=$\frac{7}{5}$DF-$\frac{5}{7}$DF=6,
解得:DF=$\frac{35}{4}$.
点评 此题属于圆的综合题.考查了切线的判定与性质、圆周角定理、垂径定理、弦切角定理、相似三角形的判定与性质以及勾股定理等知识.注意准确作出辅助线是解此题的关键.

| A. | $\frac{2016}{2015}$ | B. | -$\frac{2016}{2015}$ | C. | $\frac{2015}{2016}$ | D. | -$\frac{2015}{2016}$ |
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
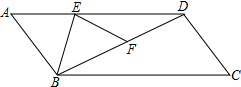 E为?ABCD边AD上一点,将△ABE沿BE翻折得到△FBE,点F在BD上,且EF=DF.若∠C=52°,那么∠ABE=51°.
E为?ABCD边AD上一点,将△ABE沿BE翻折得到△FBE,点F在BD上,且EF=DF.若∠C=52°,那么∠ABE=51°.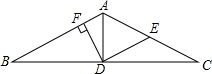 如图,在△ABC中,AB=AC,AD是△ABC点的中线,E是AC的中点,连接AC,DF⊥AB于F.求证:∠BDF=∠ADE.
如图,在△ABC中,AB=AC,AD是△ABC点的中线,E是AC的中点,连接AC,DF⊥AB于F.求证:∠BDF=∠ADE. 如图,在矩形ABCD中,AD=4,AB=3,MN∥BC分别交AB、CD于点M、N,在MN上任取两点P、Q,那么图中阴影部分的面积是6.
如图,在矩形ABCD中,AD=4,AB=3,MN∥BC分别交AB、CD于点M、N,在MN上任取两点P、Q,那么图中阴影部分的面积是6. 如图:带阴影部分的半圆的面积是多少?(π取3)
如图:带阴影部分的半圆的面积是多少?(π取3)