题目内容
12. (1)计算:-2-2-$\sqrt{(-\frac{1}{2})^{2}}$+(π-3.14)0.
(1)计算:-2-2-$\sqrt{(-\frac{1}{2})^{2}}$+(π-3.14)0.(2)解不等式组$\left\{\begin{array}{l}{2-x>0}\\{\frac{5x+1}{2}+1≥\frac{2x-1}{3}}\end{array}\right.$,并把解集在数轴上表示出来.
(3)先化简,再求值:$\frac{{a}^{2}-ab}{{a}^{2}}÷(\frac{a}{b}-\frac{b}{a}$),其中a=$\sqrt{3}$+1,b=$\sqrt{3}$-1.
分析 (1)原式第一项利用负整数指数幂法则计算,第二项利用二次根式性质计算,第三项利用零指数幂法则计算即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分,表示在数轴上即可;
(3)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把a与b的值代入计算即可求出值.
解答 解:(1)原式=-$\frac{1}{4}$-$\frac{1}{2}$+1=$\frac{1}{4}$;
(2)$\left\{\begin{array}{l}{2-x>0①}\\{\frac{5x+1}{2}+1≥\frac{2x-1}{3}②}\end{array}\right.$,
由①得:x<2;
由②得:x≥-1,
∴不等式组的解集为-1≤x<2,
(3)原式=$\frac{a(a-b)}{{a}^{2}}$÷$\frac{(a+b)(a-b)}{ab}$=$\frac{a(a-b)}{{a}^{2}}$•$\frac{ab}{(a+b)(a-b)}$=$\frac{b}{a+b}$,
当a=$\sqrt{3}$+1,b=$\sqrt{3}$-1时,原式=$\frac{\sqrt{3}-1}{\sqrt{3}+1+\sqrt{3}-1}$=$\frac{\sqrt{3}-1}{2\sqrt{3}}$=$\frac{3-\sqrt{3}}{6}$.
点评 此题考查了分式的化简求值,解一元一次不等式组,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
7.下列运算正确的是( )
| A. | 2(2x-3)=4x-3 | B. | 2x+3x=5x2 | C. | (x+1)2=x2+1 | D. | $\frac{1}{a-b}$+$\frac{1}{b-a}$=0 |
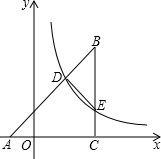 如图,等腰直角三角形ABC顶点A在x轴上,∠BCA=90°,AC=BC=2$\sqrt{2}$,反比例函数y=$\frac{3}{x}$(x>0)的图象分别与AB,BC交于点D,E.连结DE,当△BDE∽△BCA时,点E的坐标为($\frac{3}{2}\sqrt{2}$,$\sqrt{2}$).
如图,等腰直角三角形ABC顶点A在x轴上,∠BCA=90°,AC=BC=2$\sqrt{2}$,反比例函数y=$\frac{3}{x}$(x>0)的图象分别与AB,BC交于点D,E.连结DE,当△BDE∽△BCA时,点E的坐标为($\frac{3}{2}\sqrt{2}$,$\sqrt{2}$).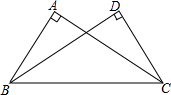 如图,∠BAC=∠CDB=90°,请你从下列条件中任选一个,使得△BAC≌△CDB,并证明.①AB=CD;②AC=DB;③∠ABC=∠DCB;④∠ACB=∠DBC.
如图,∠BAC=∠CDB=90°,请你从下列条件中任选一个,使得△BAC≌△CDB,并证明.①AB=CD;②AC=DB;③∠ABC=∠DCB;④∠ACB=∠DBC.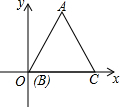 如图:正△ABC的边长为1,将一条长为2015的线段的一端固定在C处按CBAC…的规律紧绕在△ABC上,则线段的另一端点所在位置的坐标为($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
如图:正△ABC的边长为1,将一条长为2015的线段的一端固定在C处按CBAC…的规律紧绕在△ABC上,则线段的另一端点所在位置的坐标为($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).