题目内容
4.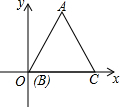 如图:正△ABC的边长为1,将一条长为2015的线段的一端固定在C处按CBAC…的规律紧绕在△ABC上,则线段的另一端点所在位置的坐标为($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
如图:正△ABC的边长为1,将一条长为2015的线段的一端固定在C处按CBAC…的规律紧绕在△ABC上,则线段的另一端点所在位置的坐标为($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
分析 根据规律发现,线段的另一端点所在位置是绕三角形几周余几个单位,利用锐角三角函数的定义,即可得出坐标.
解答 解:∵正△ABC的边长为1,
∴$\frac{2015}{3}$=671…2,
所以长为2015的线段绕三角形671周余2个单位长度,
故另一端在A处,
∵△ABC为正三角形,边长为1,
∴A点横坐标为:AO•cos60°=$\frac{1}{2}$AO=$\frac{1}{2}$,
A点纵坐标为:AO•sin60°=$\frac{\sqrt{3}}{2}$AO=$\frac{\sqrt{3}}{2}$,
A点坐标为($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
故答案为:($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
点评 本题利用点的坐标考查了数字变化规律,根据点的坐标求出三角形ABC一周的长度,从而确定2015个单位长度的细线的另一端落在第几圈第几个单位长度的位置是解题的关键.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
19.若二次根式$\sqrt{2x-4}$有意义,则x的取值范围是( )
| A. | x=2 | B. | x≠2 | C. | x≤2 | D. | x≥2 |
14.在平面直角坐标系中,已知O是原点,四边形ABCD是长方形,A,B,C的坐标分别为A(-3,1),B(-3,3),C(2,3).
(1)求D点坐标;
(2)将长方形ABCD以每秒1个单位长度的速度水平向右平移,2秒钟后所得的四边形A1B1C1D1四个顶点的坐标各是多少?
请将(1)(2)中的答案直接填入下表:
(3)平移(2)中长方形ABCD,几秒钟后△OBD的面积等于长方形ABCD的面积.
(1)求D点坐标;
(2)将长方形ABCD以每秒1个单位长度的速度水平向右平移,2秒钟后所得的四边形A1B1C1D1四个顶点的坐标各是多少?
请将(1)(2)中的答案直接填入下表:
| 点 | D | A1 | B1 | C1 | D1 |
| 坐标 |
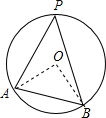 如图,A、B、P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为2$\sqrt{2}$.
如图,A、B、P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为2$\sqrt{2}$. (1)计算:-2-2-$\sqrt{(-\frac{1}{2})^{2}}$+(π-3.14)0.
(1)计算:-2-2-$\sqrt{(-\frac{1}{2})^{2}}$+(π-3.14)0.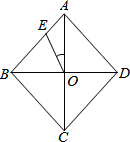 如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC、BD相交于点O,点E在AB上,且BE=BO,求∠EOA的度数.
如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC、BD相交于点O,点E在AB上,且BE=BO,求∠EOA的度数.