题目内容
4.已知抛物线y=k(x+1)(x-$\frac{3}{k}$)与x轴交于点A、B,与y轴交于点C,则能使△ABC为等腰三角形抛物线的条数是( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
分析 整理抛物线解析式,确定出抛物线与x轴的一个交点A和y轴的交点C,然后求出AC的长度,再分①k>0时,点B在x轴正半轴时,分AC=BC、AC=AB、AB=BC三种情况求解;②k<0时,点B在x轴的负半轴时,点B只能在点A的左边,只有AC=AB一种情况列式计算即可.
解答 解:y=k(x+1)(x-$\frac{3}{k}$)=(x+1)(kx-3),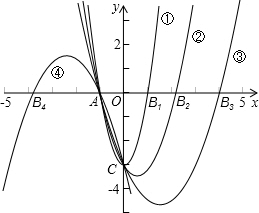
所以,抛物线经过点A(-1,0),C(0,-3),
AC=$\sqrt{{OA}^{2}{+OC}^{2}}$=$\sqrt{{1}^{2}{+3}^{2}}$=$\sqrt{10}$,
点B坐标为($\frac{3}{k}$,0),
①k>0时,点B在x正半轴上,
若AC=BC,则$\sqrt{(\frac{3}{k})^{2}{+3}^{2}}$=$\sqrt{10}$,解得k=3,
若AC=AB,则$\frac{3}{k}$+1=$\sqrt{10}$,解得k=$\frac{3}{\sqrt{10}-1}$=$\frac{\sqrt{10}+1}{3}$,
若AB=BC,则$\frac{3}{k}$+1=$\sqrt{(\frac{3}{k})^{2}{+3}^{2}}$,解得k=$\frac{3}{4}$;
②k<0时,点B在x轴的负半轴,点B只能在点A的左侧,
只有AC=AB,则-1-$\frac{3}{k}$=$\sqrt{10}$,解得k=-$\frac{3}{\sqrt{10}+1}$=-$\frac{\sqrt{10}-1}{3}$,
所以,能使△ABC为等腰三角形的抛物线共有4条.
故选B.
点评 本题考查了抛物线与x轴的交点问题,根据抛物线的解析式确定出抛物线经过的两个定点是解题的关键,注意分情况讨论.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目
 如图,某数学兴趣小组将周长为12的正方形铁丝框变形为一个扇形框,则所得扇形的面积的最大值为9.
如图,某数学兴趣小组将周长为12的正方形铁丝框变形为一个扇形框,则所得扇形的面积的最大值为9.
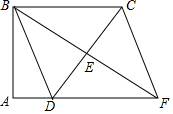 如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,点E是边CD的中点,连接BE并延长交AD的延长线于点F,连接CF.
如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,点E是边CD的中点,连接BE并延长交AD的延长线于点F,连接CF.