题目内容
14．
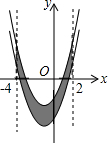如图，已知抛物线y=x2+2x-3，把此抛物线沿y轴向下平移，平移后的抛物线和原抛物线与经过点（-4，0），（2，0）且平行于y轴的两条直线所围成的阴影部分的面积为s，平移的距离为m，则s与m的函数关系式为s=6m（不写自变量取值范围）．
分析 根据图形平移后面积不变的性质，可把不规则阴影部分的面积转化为规则图形（矩形）即可判断．
解答 解：我们把抛物线沿y轴向上平移，平移后的抛物线和原抛物线及直线x=2，x=-4所围成的阴影部分的面积s可以看做和矩形等积，
于是可以看出S与m是正比例函数关系：s=6m．
故答案是：s=6m．
点评 本题主要考查了函数图象与几何变换：由于抛物线平移后的形状不变，因此可把平移后不规则图形转化为规则图形解决问题．
练习册系列答案
相关题目
将正奇数按如右上图所示规律排列下去．若用有序数对（n，m）表示实数9，则（6，3）表示的数是35．2011是（45，16）．
观察如图所示的三角形数阵，当最下面一行的两个数为多少时，这两个数以及它们上面的数的个数为2015？
9．
如图，若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{1}{x}$（x＞0）的图象上，则点E的坐标是（ ）
如图，若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{1}{x}$（x＞0）的图象上，则点E的坐标是（ ）| A． | （4，1） | B． | （3，$\frac{4}{3}$） | C． | （$\frac{\sqrt{5}+1}{2}$，$\frac{\sqrt{5}-1}{2}$） | D． | （$\sqrt{6}+\sqrt{2}$，$\sqrt{6}-\sqrt{2}$） |
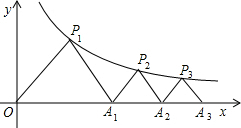如图，△P1OA1，△P2A1A2，△P3A2A3…△PnAn-1An都是等腰直角三角形，点P1、P2、P3…Pn都在函数$y=\frac{4}{x}$（x＞0）的图象上，斜边OA1、A1A2、A2A3…An-1An都在x轴上．则点P12的坐标是（4$\sqrt{3}$+2$\sqrt{11}$，4$\sqrt{3}$-2$\sqrt{11}$）．
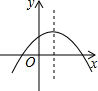已知二次函数y=ax2+bx+c（x≠0）的图象如图所示，则正比例函数y=（b+c）x的图象与反比例函数y=$\frac{a}{x}$的图象在同一坐标系中可能是（ ）
4．在平面直角坐标系中，已知点A（0，2），⊙A的半径是2，⊙P的半径是1，满足与⊙A及x轴都相切的⊙P有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |