题目内容
19.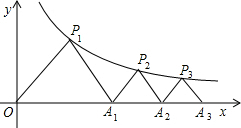 如图,△P1OA1,△P2A1A2,△P3A2A3…△PnAn-1An都是等腰直角三角形,点P1、P2、P3…Pn都在函数$y=\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A2、A2A3…An-1An都在x轴上.则点P12的坐标是(4$\sqrt{3}$+2$\sqrt{11}$,4$\sqrt{3}$-2$\sqrt{11}$).
如图,△P1OA1,△P2A1A2,△P3A2A3…△PnAn-1An都是等腰直角三角形,点P1、P2、P3…Pn都在函数$y=\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A2、A2A3…An-1An都在x轴上.则点P12的坐标是(4$\sqrt{3}$+2$\sqrt{11}$,4$\sqrt{3}$-2$\sqrt{11}$).
分析 根据等腰直角三角形的性质,知P1的横、纵坐标相等,再结合双曲线的解析式求得该点的纵坐标;根据等腰直角三角形的性质和双曲线的解析式首先求得各个点的横坐标,再进一步求得其纵坐标,发现其的规律,从而求得点P12的坐标.
解答 解:由△P1OA1是等腰直角三角形,得y1=x1,
则有y12=4,故y1=±2(负舍),则y1=2.
由题意知y2=x2-x1-y1,y3=x3-x2-y2,y4=x4-x3-y3,…,y10=x10-x9-y9,
又∵yn=$\frac{4}{{x}_{n}}$,则:x2-4=$\frac{4}{{x}_{2}}$,解得x2=2$\sqrt{2}$+2.
∴y2=2$\sqrt{2}$-2,
同理,依次得 x3=2$\sqrt{3}$+2$\sqrt{2}$,y3=2$\sqrt{3}$-2$\sqrt{2}$,
x4=2$\sqrt{4}$+2$\sqrt{3}$,y4=2$\sqrt{4}$-2$\sqrt{3}$,
x5=2$\sqrt{5}$+2$\sqrt{4}$,y5=2$\sqrt{5}$-2$\sqrt{4}$,
…
xn=2$\sqrt{n}$+2$\sqrt{n-1}$,yn=2$\sqrt{n}$-2$\sqrt{n-1}$,
∴x12=2$\sqrt{12}$+2$\sqrt{11}$,y12=2$\sqrt{12}$-2$\sqrt{11}$,
∴P(4$\sqrt{3}$+2$\sqrt{11}$,4$\sqrt{3}$-2$\sqrt{11}$).
故答案为(4$\sqrt{3}$+2$\sqrt{11}$,4$\sqrt{3}$-2$\sqrt{11}$).
点评 此题主要是综合考查了等腰直角三角形的性质以及结合反比例函数的解析式求得点的坐标.解答本题时同学们要找出其中的规律.

| A. | 两条对角线互相平分的四边形是平行四边形 | |
| B. | 两条对角线互相垂直的四边形是菱形 | |
| C. | 两条对角线互相垂直且相等的四边形是正方形 | |
| D. | 两条对角线相等的四边形是矩形 |
| A. | 10℃ | B. | 40℃ | C. | -10℃ | D. | -40℃ |
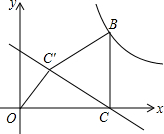 点C在x的正半轴上,且BC⊥OC于点C,将线段BC绕点B顺时针旋转60°至BC′位置,且点C′的坐标为(2,2$\sqrt{3}$).
点C在x的正半轴上,且BC⊥OC于点C,将线段BC绕点B顺时针旋转60°至BC′位置,且点C′的坐标为(2,2$\sqrt{3}$).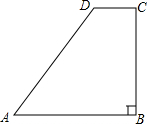 如图,在直角梯形ABCD中,∠DCB=90°,AB∥CD,AB=25,BC=24.将该梯形沿过B点的直线折叠,使A点恰好与D点重合,BE为折痕.
如图,在直角梯形ABCD中,∠DCB=90°,AB∥CD,AB=25,BC=24.将该梯形沿过B点的直线折叠,使A点恰好与D点重合,BE为折痕.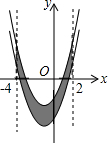 如图,已知抛物线y=x2+2x-3,把此抛物线沿y轴向下平移,平移后的抛物线和原抛物线与经过点(-4,0),(2,0)且平行于y轴的两条直线所围成的阴影部分的面积为s,平移的距离为m,则s与m的函数关系式为s=6m(不写自变量取值范围).
如图,已知抛物线y=x2+2x-3,把此抛物线沿y轴向下平移,平移后的抛物线和原抛物线与经过点(-4,0),(2,0)且平行于y轴的两条直线所围成的阴影部分的面积为s,平移的距离为m,则s与m的函数关系式为s=6m(不写自变量取值范围).