题目内容
4. 如图,已知AB∥CD,BC平分∠ABE,∠C=32°,则∠BED的度数是64°.
如图,已知AB∥CD,BC平分∠ABE,∠C=32°,则∠BED的度数是64°.
分析 根据平行线的性质得到∠ABC=∠C=32°,再根据角平分线的定义得到∠ABC=∠EBC=32°,然后利用三角形外角性质计算即可.
解答 解:∵AB∥CD,
∴∠ABC=∠C=32°,
又∵BC平分∠ABE,
∴∠ABC=∠EBC=32°,
∴∠BED=∠C+∠EBC=32°+32°=64°.
故答案为:64°.
点评 本题考查了平行线的性质:两直线平行,内错角相等.也考查了三角形外角性质以及角平分线的定义.

练习册系列答案
相关题目
15. 如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )
如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )
 如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )
如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )| A. | x>-2 | B. | x<-2 | C. | -3<x<-2 | D. | -3<x<-1 |
9.下列能够判定一个四边形是正方形的条件是( )
①一组邻边相等且对角线相等并互相平分;
②对角线互相垂直平分;
③四条边相等且四个内角也相等;
④对角线相等的菱形.
①一组邻边相等且对角线相等并互相平分;
②对角线互相垂直平分;
③四条边相等且四个内角也相等;
④对角线相等的菱形.
| A. | ①②④ | B. | ①③④ | C. | ③④ | D. | ①②③④ |
 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,O、M也在格点上.
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,O、M也在格点上.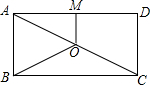 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=3,AD=4,则四边形ABOM的周长为9.
如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=3,AD=4,则四边形ABOM的周长为9. 如图,正方形ABCD的边长为2,对角线AC、BD相交于点O,将△AOD沿着AD翻折,点O恰好落在点E.
如图,正方形ABCD的边长为2,对角线AC、BD相交于点O,将△AOD沿着AD翻折,点O恰好落在点E. 如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠A=40°.
如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠A=40°.