题目内容
14.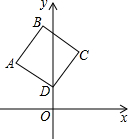 如图,在正方形ABCD中,点D的坐标为(0,1),点A的坐标是(-2,2),则点B的坐标为(-1,4).
如图,在正方形ABCD中,点D的坐标为(0,1),点A的坐标是(-2,2),则点B的坐标为(-1,4).
分析 过点A作AF⊥y轴,垂足为F,过点B作BE⊥AF,垂足为E.先证明△ABE≌△DAF,由全等三角形的性质可知DF=AE=1,AF=BE=2,于是可得到点B的坐标.
解答 解:如图所示:过点A作AF⊥y轴,垂足为F,过点B作BE⊥AF,垂足为E.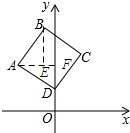
∵点D的坐标为(0,1),点A的坐标是(-2,2),
∴DF=1,AF=2.
∵四边形ABCD为正方形,
∴∠BAD=90°,AB=AD.
∵∠BAE+∠DAF=90°,∠DAF+∠ADF=90°,
∴∠BAE=∠ADF.
∵在△ABE和△DAF中$\left\{\begin{array}{l}{∠BAE=∠ADF}\\{∠AEB=∠AFD}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△DAF.
∴DF=AE=1,AF=BE=2
∴EF=2-1=1,OF+BE=4.
∴B(-1,4).
故答案为:(-1,4).
点评 本题主要考查的是正方形的性质、全等三角形的性质和判定,掌握此类问题的辅助线的作法是解题的关键.

练习册系列答案
相关题目
4.下列命题中,是假命题的是( )
| A. | 等角的余角相等 | B. | 若a>b,且m≠0,则am>bm | ||
| C. | 三角形的外角和等于360° | D. | 两直线平行,同位角相等 |
2.某班学生参加运土劳动,一部分学生抬土,另一部分学生挑土,已知全班共用箩筐99个,扁担66根,求抬土、挑土的学生各有多少人?如果设抬土的同学x人,挑土的同学y人,则可得方程组( )
| A. | $\left\{\begin{array}{l}{2(x+\frac{y}{2})=99}\\{\frac{x}{2}+y=66}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+y=66}\\{\frac{x}{2}+y=99}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{x}{2}+y=66}\\{\frac{x}{2}+2y=99}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+2y=99}\\{2x+y=66}\end{array}\right.$ |
9.在函数y=$\sqrt{x-1}$中,x的取值范围是( )
| A. | x≥1 | B. | x≤1 | C. | x≠1 | D. | x<0 |
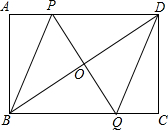 如图,矩形ABCD中,O为BD中点,PQ过点P分别交AD、BC于点P、Q,连接BP和DQ,求证:四边形PBQD是平行四边形.
如图,矩形ABCD中,O为BD中点,PQ过点P分别交AD、BC于点P、Q,连接BP和DQ,求证:四边形PBQD是平行四边形. 如图,直角三角形的两条直角边AC,BC分别经过正九边形的两个顶点,则图中∠1+∠2的结果是190°.
如图,直角三角形的两条直角边AC,BC分别经过正九边形的两个顶点,则图中∠1+∠2的结果是190°.