题目内容
8.在同一直角坐标系中,画出函数y=-$\frac{1}{2}$x2,y=-$\frac{1}{2}$x2-1,y=-$\frac{1}{2}$(x+1)2-1的图象,并列表比较这三条抛物线的对称轴、顶点坐标.分析 利用描点法可画出这三个函数的图象;分别由图象可得出对称轴及顶点坐标.
解答 解:三个函数的图象如图所示:
由图象可知函数y=-$\frac{1}{2}$x2的对称轴为x=0,顶点坐标为(0,0);
函数y=-$\frac{1}{2}$x2-1的对称轴为x=0,顶点坐标为(0,-1);
函数y=-$\frac{1}{2}$(x+1)2-1的对称轴为x=-1,顶点坐标为(-1,-1).
点评 本题主要考查函数图象的画法及二次函数的图象的性质,掌握基本的描点法作函数图象是解题的关键.

练习册系列答案
相关题目
13.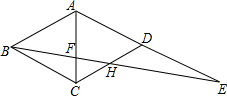 如图,四边形ABCD是菱形,其边长AB=5,点E为AD的延长线上一点,连接BE,分别交AC、DC于点F、H,BF=DE,FH=2,则DE的长为( )
如图,四边形ABCD是菱形,其边长AB=5,点E为AD的延长线上一点,连接BE,分别交AC、DC于点F、H,BF=DE,FH=2,则DE的长为( )
 如图,四边形ABCD是菱形,其边长AB=5,点E为AD的延长线上一点,连接BE,分别交AC、DC于点F、H,BF=DE,FH=2,则DE的长为( )
如图,四边形ABCD是菱形,其边长AB=5,点E为AD的延长线上一点,连接BE,分别交AC、DC于点F、H,BF=DE,FH=2,则DE的长为( )| A. | 2 | B. | 3 | C. | $\frac{10}{3}$ | D. | $\frac{13}{3}$ |
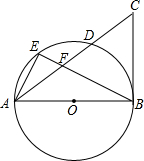 如图,AB是⊙O的直径,BC是⊙O的切线,连接AC交⊙O于点D,E为$\widehat{AD}$上一点,连结AE、BE,BE交AC于点F,且∠AFE=∠EAB.
如图,AB是⊙O的直径,BC是⊙O的切线,连接AC交⊙O于点D,E为$\widehat{AD}$上一点,连结AE、BE,BE交AC于点F,且∠AFE=∠EAB. 如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=2,则线段ON的长为1.
如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=2,则线段ON的长为1.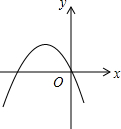 二次函数y=ax2+bx+c的图象如图,解不等式bx+a>0.
二次函数y=ax2+bx+c的图象如图,解不等式bx+a>0.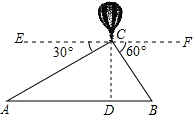 如图所示,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,已知AB间的距离为180米,CD垂直于AB于点D.问:此时热气球的高度为多少?
如图所示,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,已知AB间的距离为180米,CD垂直于AB于点D.问:此时热气球的高度为多少? 如图,AB是⊙O的直径,∠D=20°.求∠BAC的度数.
如图,AB是⊙O的直径,∠D=20°.求∠BAC的度数.