题目内容
19．
如图，AB是⊙O的直径，∠D=20°．求∠BAC的度数．
分析 连结BC，根据圆周角定理及已知可求得∠B、∠ACB的度数，再根据三角形内角和公式即可求得∠BAC的度数．
解答 
解：连结BC，
∵AB是半圆O的直径（已知），
∴∠ACB=90°（直径所对的圆周角是直角）；
∵∠ADC=20°（已知），
∴∠B=20°（同弧所对的圆周角相等），
∴∠BAC=180°-∠B-∠ACB=180°-90°-20°=70°．
点评 本题考查了圆周角定理．解答该题时，利用了三角形的内角和定理，直径对的圆周角是直角求解．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
10．
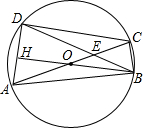如图，四边形ABCD内接于⊙O，对角线AC经过圆心O．且交BD于点E，BO⊥AD于点H，OA=AD=2，则OE：EC值是（ ）
如图，四边形ABCD内接于⊙O，对角线AC经过圆心O．且交BD于点E，BO⊥AD于点H，OA=AD=2，则OE：EC值是（ ）| A． | 1：2 | B． | 1：$\sqrt{2}$ | C． | 1：$\sqrt{3}$ | D． | $\sqrt{2}$：$\sqrt{3}$ |
11．公式：（x+y+z）2=x2+y2+z2+2（xy+yz+xz）．若现有三实数a、b、c，满足a+b+c=0，abc=6，则$\frac{1}{a}$$+\frac{1}{b}$$+\frac{1}{c}$为（ ）
| A． | 正数 | B． | 负数 | C． | 零 | D． | 非负数 |
8．如图所示是一天中不同时刻直立的灯杆在阳光下形成的影长，规定各图向右为正东方向，将各图按时间顺序排列正确的是（ ）
| A． | ②④①③ | B． | ③①④② | C． | ②④③① | D． | ①③②④ |
9．下列方程是二元一次方程的是（ ）
| A． | y=x+8 | B． | $\frac{4}{x}+y=5$ | C． | $\frac{1}{2}{x}^{2}+y=0$ | D． | 2x+3y=z |