题目内容
8. 如图,△ABC中,AB=AC=10,BC=12,动点P从A点出发,按A→B的方向在AB上移动,动点Q从B点出发,按B→C的方向在BC上移动(当P点到达点B时,P点和Q点停止移动,且两点的移动速度相等),记PA=x,△BPQ的面积为y,则y关于x的函数图象大致是( )
如图,△ABC中,AB=AC=10,BC=12,动点P从A点出发,按A→B的方向在AB上移动,动点Q从B点出发,按B→C的方向在BC上移动(当P点到达点B时,P点和Q点停止移动,且两点的移动速度相等),记PA=x,△BPQ的面积为y,则y关于x的函数图象大致是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据题意可以分别求得BP和点P到BC的距离,从而可以将△BPQ的面积表示出来,从而可以得到哪个函数的图象是正确的.
解答  解:分别过点A、点P作AD⊥BC于点D,PE⊥BC于点E,如右图所示,
解:分别过点A、点P作AD⊥BC于点D,PE⊥BC于点E,如右图所示,
∵∠PBE=∠ABD,∠PEB=∠ADB=90°,
∴△PBE∽△ABD,
∴$\frac{PB}{AB}=\frac{PE}{AD}$,
即$\frac{10-x}{10}=\frac{PE}{8}$,
解得,PE=$8-\frac{4}{5}x$,
∴$y=\frac{1}{2}x(8-\frac{4}{5}x)=-\frac{2}{5}(x-5)^{2}+10$(0≤x≤10),
故选B.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17. 如图,正△ABC的边长是2,分别以点B、C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当$\sqrt{2}≤r<2$时,S的取值范围是( )
如图,正△ABC的边长是2,分别以点B、C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当$\sqrt{2}≤r<2$时,S的取值范围是( )
 如图,正△ABC的边长是2,分别以点B、C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当$\sqrt{2}≤r<2$时,S的取值范围是( )
如图,正△ABC的边长是2,分别以点B、C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当$\sqrt{2}≤r<2$时,S的取值范围是( )| A. | $\frac{π}{2}$-1≤S<$\frac{4π}{3}$-$\sqrt{3}$ | B. | $\frac{π}{2}$-1≤S<$\frac{4π}{3}$-1 | C. | 1≤S<$\sqrt{3}$ | D. | $\sqrt{3}≤S$$<2\sqrt{3}$-1 |
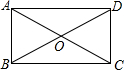 如图,矩形ABCD的对角线相交于O,要使它成为正方形,应添加的条件是AB=BC(只填写一个条件即可)
如图,矩形ABCD的对角线相交于O,要使它成为正方形,应添加的条件是AB=BC(只填写一个条件即可)


