题目内容
3.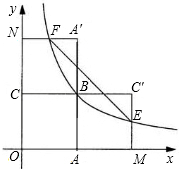 如图,正方形OABC的面积为4,反比例函数$y=\frac{k}{x}$(x>0)的图象经过点B.
如图,正方形OABC的面积为4,反比例函数$y=\frac{k}{x}$(x>0)的图象经过点B.(1)求点B的坐标和k的值;
(2)将正方形OABC分别沿直线AB、BC翻折,得到正方形AMC′B、CBA′N.设线段MC′、NA′分别与函数$y=\frac{k}{x}$(x>0)的图象交于点E、F,求直线EF的解析式.
分析 (1)由正方形的面积公式可求出点B的坐标,将点B的坐标代入反比例函数关系式中可得出关于k的一元一次方程,解方程即可得出结论;
(2)由翻折的性质可得出点E的横坐标、点F的纵坐标,由E、F点在反比例函数上可得出E、F点的坐标,设出直线EF解析式为y=mx+n,由待定系数法即可求出直线EF的解析式.
解答 解:(1)∵正方形OABC的面积为4,
∴OA=OC=2,
∴点B坐标为(2,2).
∵$y=\frac{k}{x}$的图象经过点B,
∴k=xy=2×2=4.
(2)∵正方形AMC′B、CBA′N由正方形OABC翻折所得,
∴ON=OM=2OA=4,
∴点E横坐标为4,点F纵坐标为4.
∵点E、F在函数y=$\frac{4}{x}$的图象上,
∴当x=4时,y=1,即E(4,1);
当y=4时,x=1,即F(1,4).
设直线EF解析式为y=mx+n,将E、F两点坐标代入,
得$\left\{\begin{array}{l}4m+n=1\\ m+n=4.\end{array}\right.$,
∴m=-1,n=5.
∴直线EF解析式为y=-x+5.
点评 本题考查了待定系数法求函数解析式、反比例函数与一次函数的交点问题以及翻折变换,解题的关键是:(1)求出点B的坐标;(2)求出E、F点的坐标.本题属于基础题,难度不大,解决该题型题目时,结合点的坐标利用待定系数法求函数解析式是关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
11.关于x的一元二次方程(a-1)x2-2x+3=0没有实数根,则整数a的最小值是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
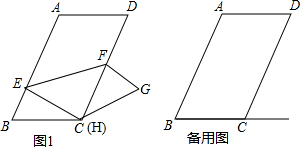
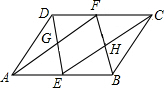 如图,在?ABCD中,E,F分别是AB,CD的中点,连结DE,AF,CF,BF,分别相交于点G,H.试说明四边形EHFG是平行四边形.
如图,在?ABCD中,E,F分别是AB,CD的中点,连结DE,AF,CF,BF,分别相交于点G,H.试说明四边形EHFG是平行四边形.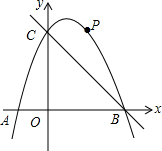 如图,在平面直角坐标系中,二次函数y=-x2+bx+c的图象与x轴交于A、B两点,与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0).点P是抛物线上一个动点,且在直线BC的上方.
如图,在平面直角坐标系中,二次函数y=-x2+bx+c的图象与x轴交于A、B两点,与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0).点P是抛物线上一个动点,且在直线BC的上方.