题目内容
14. 如图所示,一架云梯AB斜靠在一面墙上,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿底面向右滑行.
如图所示,一架云梯AB斜靠在一面墙上,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿底面向右滑行.(1)请判断木棍滑动的过程中,点P到点O的距离是否变化,并简述理由;
(2)若梯子底端B离墙7米,如果梯子的顶端A下滑4米至A′处,那么梯子的底部在水平方向滑动8米至B′处,求梯子的长度.
分析 (1)利用直角三角形的性质得出OP=$\frac{1}{2}$AB,进而得出答案;
(2)利用梯子的总长不变得出等式,进而利用勾股定理得出答案.
解答 解:(1)点P到点O的距离不变化,
理由:∵木棍的中点为P,△AOB为直角三角形,
∴OP=$\frac{1}{2}$AB,即点P到点O的距离不变化;
(2)由题意可得:BO=7m,BB′=8m,AA′=4m,
故设AO=xm,则OA′=(x-4)m,
则72+x2=(x-4)2+152,
解得:x=24,
故AB=$\sqrt{2{4}^{2}+{7}^{2}}$=25(m),
答:梯子的长度为25m.
点评 此题主要考查了勾股定理的应用以及直角三角形的性质,利用梯子的总长不变得出等式是解题关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 如图,AB=AC,E是线段AB的三分之一点,∠ADB=90°,求证:点F是AD的中点.
如图,AB=AC,E是线段AB的三分之一点,∠ADB=90°,求证:点F是AD的中点.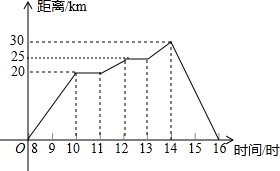 假日里,小亮和爸爸骑自行车郊游,上午8时从家出发,16时返回家中,他们离家的距离与时间的关系可用图中的折线表示.
假日里,小亮和爸爸骑自行车郊游,上午8时从家出发,16时返回家中,他们离家的距离与时间的关系可用图中的折线表示.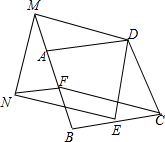 如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF.
如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF.