题目内容
12.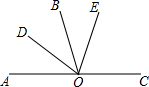 已知,O是直线AC上一点,OD平分∠AOB,∠BOE=$\frac{1}{2}$∠EOC,∠DOE=72°,OB是∠DOE的平分线吗?说明理由.
已知,O是直线AC上一点,OD平分∠AOB,∠BOE=$\frac{1}{2}$∠EOC,∠DOE=72°,OB是∠DOE的平分线吗?说明理由.
分析 设∠EOB=x度,∠EOC=2x度,把角用未知数表示出来,建立x的方程,求出x的值,进而可得结论.
解答 解:OB是∠DOE的平分线;
理由:设∠EOB=x,则∠EOC=2x,
则∠BOD=$\frac{1}{2}$(180°-3x),
∵∠BOE+∠BOD=∠DOE,
∴x+$\frac{1}{2}$(180°-3x)=72°,
解得x=36°,
∴∠EOB=36°,
∴∠BOD=$\frac{1}{2}$(180°-3×36°)=36°,
∴OB是∠DOE的平分线.
点评 此题主要考查了角平分线的定义,关键是掌握角平分线把角分成相等的两部分.

练习册系列答案
相关题目
20.2013年中考结束后,某市从参加中考的52000名学生中抽取600名学生的数学成绩(考生得分均为整数,满分150分)进行统计,则此次抽样调查的样本是抽取600名学生的数学成绩,样本容量是600.
2.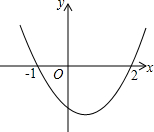 如图,抛物线y=ax2+bx+c与x轴的交点坐标是(-1,0)与(2,0),若x1,x2 (x1<x2)是方程ax2+bx+c=n(c<n<0)的两个实数根,则x1,x2的取值范围是( )
如图,抛物线y=ax2+bx+c与x轴的交点坐标是(-1,0)与(2,0),若x1,x2 (x1<x2)是方程ax2+bx+c=n(c<n<0)的两个实数根,则x1,x2的取值范围是( )
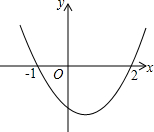 如图,抛物线y=ax2+bx+c与x轴的交点坐标是(-1,0)与(2,0),若x1,x2 (x1<x2)是方程ax2+bx+c=n(c<n<0)的两个实数根,则x1,x2的取值范围是( )
如图,抛物线y=ax2+bx+c与x轴的交点坐标是(-1,0)与(2,0),若x1,x2 (x1<x2)是方程ax2+bx+c=n(c<n<0)的两个实数根,则x1,x2的取值范围是( )| A. | x1<-1,x2>2 | B. | -1<x1<0<x2 | C. | x1<0<x2<2 | D. | -1<x1<0且0<x2<2 |
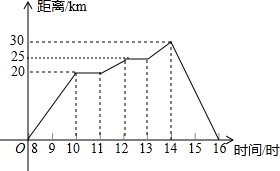 假日里,小亮和爸爸骑自行车郊游,上午8时从家出发,16时返回家中,他们离家的距离与时间的关系可用图中的折线表示.
假日里,小亮和爸爸骑自行车郊游,上午8时从家出发,16时返回家中,他们离家的距离与时间的关系可用图中的折线表示.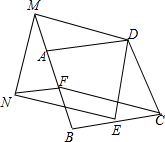 如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF.
如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF.