题目内容
4. 某公司购进一种商品的成本为30元/kg,经市场调研发现,这种商品在未来90
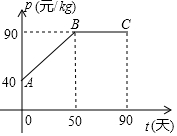
某公司购进一种商品的成本为30元/kg,经市场调研发现,这种商品在未来90天的销售单价p(元/kg)与时间t(天)之间的相关信息如下图,销售量y(kg)与时间t(天)之间满足一次函数关系,且对应数据如下表.设第t天的销售利润为w(元)
| 时间t(天) | 10 | 30 |
| 每天的销售量 y(kg) | 180 | 140 |
(2)问:销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)在实际销售的前50天中,公司决定每销售1kg该商品就捐赠n元利润(n<12)给“精准扶贫”对象.现发现:在前50天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
分析 (1)直接利用待定系数法求出一次函数解析式,进而得出答案;
(2)利用销量×每千克利润=总利润,进而求出答案;
(3)利用二次函数增减性结合对称轴公式得出n的取值范围.
解答 解:(1)设y=kt+b,把t=10,y=180;t=30,y=140代入得到:
$\left\{\begin{array}{l}{10k+b=180}\\{30k+b=140}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=200}\end{array}\right.$,
∴y=-2t+200.
当0<t<50时,设p=kt+40,由图象得B(50,90)
∴50k+40=90,
∴k=1,
∴p=t+40,
当50≤t≤90时,p=90;
(2)由题意可得:w=(-2t+200)(t+40-30)
=-2t2+180t+2000
=-2(t-45)2+6050,
∴t=45时,w最大值为6050元,
w=(-2t+120)(90-30)=-120t+12000,
∵-120<0,
∴w随x增大而减小,
∴t=50时,w最大值=6000,
综上所述第45天利润最大,最大利润为6050元;
(3)设前50天每天扣除捐赠后的日销售利润为m元.
由题意m=-2t2+180t+2000-(-2t+200)n
=-2t2+(180+2n)t+2000-200n,
∵在前50天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,
∴-$\frac{b}{2a}$=-$\frac{180+2n}{-4}$≥50,
∴n≥10.
又∵n<12,
∴n的取值范围为:10≤n<12.
点评 此题主要考查了二次函数的应用,熟练掌握各函数的性质和图象特征,最值问题需由函数的性质求解时,正确表达关系式是关键.

| A. | $-\frac{1}{3}$ | B. | -3 | C. | 3 | D. | $\frac{1}{3}$ |
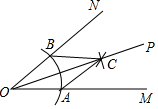 如图,用尺规作∠MON的平分线OP.由作图知△OAC≌△OBC,从而得OP平分∠MON,则此两个三角形全等的依据是( )
如图,用尺规作∠MON的平分线OP.由作图知△OAC≌△OBC,从而得OP平分∠MON,则此两个三角形全等的依据是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
| A. | 测量该四边形的对角线是否互相垂直 | |
| B. | 测量该四边形的对角线是否相等 | |
| C. | 测量该四边形的对角线是否互相平分 | |
| D. | 测量该四边形的四条边是否都相等 |
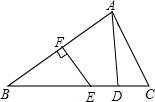 如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.
如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.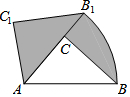 如图,在△ACB中,∠BAC=50°,AC=4,AB=6.现将△ACB绕点A逆时针旋转50°得到△AC1B1则阴影部分的面积为5π.
如图,在△ACB中,∠BAC=50°,AC=4,AB=6.现将△ACB绕点A逆时针旋转50°得到△AC1B1则阴影部分的面积为5π. 如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1>mx+n的解集为x>1.
如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1>mx+n的解集为x>1.