题目内容
9．
如图，直线l1：y=x+1与直线l2：y=mx+n相交于点P（a，2），则关于x的不等式x+1＞mx+n的解集为x＞1．
分析 首先将已知点的坐标代入直线y=x+1求得a的值，然后观察函数图象得到在点P的右边，直线y=x+1都在直线y=mx+n的上方，据此求解．
解答 解：∵直线l1：y=x+1与直线l2：y=mx+n相交于点P（a，2），
∴a+1=2，
解得：a=1，
观察图象知：关于x的不等式x+1＞mx+n的解集为x＞1，
故答案为x＞1．
点评 此题主要考查了一次函数与一元一次不等式，关键是求出两函数图象的交点坐标，根据函数图象可得答案．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
20．计算（a-2）（-a-2）的结果正确的是（ ）
| A． | a2-4 | B． | a2-4a+4 | C． | 4-a2 | D． | 2-a2 |
如图，AB是⊙O的直径，C、D是⊙O上的两点，若∠ABD=62°，则∠BCD=28°．
4．
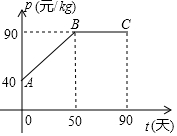某公司购进一种商品的成本为30元/kg，经市场调研发现，这种商品在未来90
天的销售单价p（元/kg）与时间t（天）之间的相关信息如下图，销售量y（kg）与时间t（天）之间满足一次函数关系，且对应数据如下表．设第t天的销售利润为w（元）
（1）分别求出售单价p（元/kg）、销售量y（kg）与时间t（天）之间的函数关系式；
（2）问：销售该商品第几天时，当天的销售利润最大？并求出最大利润；
（3）在实际销售的前50天中，公司决定每销售1kg该商品就捐赠n元利润（n＜12）给“精准扶贫”对象．现发现：在前50天中，每天扣除捐赠后的日销售利润随时间t的增大而增大，求n的取值范围．
某公司购进一种商品的成本为30元/kg，经市场调研发现，这种商品在未来90天的销售单价p（元/kg）与时间t（天）之间的相关信息如下图，销售量y（kg）与时间t（天）之间满足一次函数关系，且对应数据如下表．设第t天的销售利润为w（元）
| 时间t（天） | 10 | 30 |
| 每天的销售量 y（kg） | 180 | 140 |
（2）问：销售该商品第几天时，当天的销售利润最大？并求出最大利润；
（3）在实际销售的前50天中，公司决定每销售1kg该商品就捐赠n元利润（n＜12）给“精准扶贫”对象．现发现：在前50天中，每天扣除捐赠后的日销售利润随时间t的增大而增大，求n的取值范围．
如图，在平面直角坐标系中，点A、B、C的坐标分别为（-1，3）、（-4，1）、（-2，1），先将△ABC沿一确定方向平移得到△A1B1C1，点B的对应点B1的坐标是（1，2），再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2，点A1的对应点为点A2．
1．下列说法正确的是（ ）
| A． | 射线AB与射线BA是同一条射线 | |
| B． | 任何一个锐角的余角比它的补角小90° | |
| C． | 一个角的补角一定大于这个角 | |
| D． | 如果∠1+∠2+∠3=180°，那么∠1、∠2、∠3互为补角 |
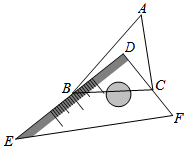有一块直角三角板DEF放置在△ABC上，三角板DEF的两条直角边DE、DF恰好分别经过点B、C．△ABC中，∠A=50°，求∠DBA+∠DCA的度数．