题目内容
14.在数学活动课上,同学们用木条做成一个四边形框架,要判断该四边形是否为菱形,下列测量方案可行的是( )| A. | 测量该四边形的对角线是否互相垂直 | |
| B. | 测量该四边形的对角线是否相等 | |
| C. | 测量该四边形的对角线是否互相平分 | |
| D. | 测量该四边形的四条边是否都相等 |
分析 根据菱形的判定定理分别进行解答即可得出答案.菱形的判定定理有:(1)邻边相等的平行四边形是菱形;(2)四条边都相等的四边形是菱形;(3)对角线互相垂直的平行四边形的四边形是菱形.
解答 解:A、对角线是否相等,只能判定矩形或等腰梯形;
B、对角线是否相等不能判定形状;
C、对角线互相平分只能判定平行四边形,不能判定菱形;
D、其中四边形的四条边都相等,能判定菱形.
故选D.
点评 此题考查了菱形的判定,用到的知识点是菱形的判定定理,难度不大.

练习册系列答案
相关题目
4. 某公司购进一种商品的成本为30元/kg,经市场调研发现,这种商品在未来90
某公司购进一种商品的成本为30元/kg,经市场调研发现,这种商品在未来90
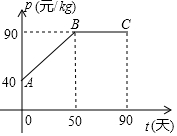
天的销售单价p(元/kg)与时间t(天)之间的相关信息如下图,销售量y(kg)与时间t(天)之间满足一次函数关系,且对应数据如下表.设第t天的销售利润为w(元)
(1)分别求出售单价p(元/kg)、销售量y(kg)与时间t(天)之间的函数关系式;
(2)问:销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)在实际销售的前50天中,公司决定每销售1kg该商品就捐赠n元利润(n<12)给“精准扶贫”对象.现发现:在前50天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
 某公司购进一种商品的成本为30元/kg,经市场调研发现,这种商品在未来90
某公司购进一种商品的成本为30元/kg,经市场调研发现,这种商品在未来90天的销售单价p(元/kg)与时间t(天)之间的相关信息如下图,销售量y(kg)与时间t(天)之间满足一次函数关系,且对应数据如下表.设第t天的销售利润为w(元)
| 时间t(天) | 10 | 30 |
| 每天的销售量 y(kg) | 180 | 140 |
(2)问:销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)在实际销售的前50天中,公司决定每销售1kg该商品就捐赠n元利润(n<12)给“精准扶贫”对象.现发现:在前50天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
9.小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息,a-b,x-y,x+y,a+b,x2-y2,a2-b2分别对应下列六个字:台、爱、我、邢、游、美,现将(x2-y2)a2-(x2-y2)b2因式分解,结果呈现的密码信息可能是( )
| A. | 我爱美 | B. | 邢台游 | C. | 爱我邢台 | D. | 美我邢台 |
6.已知两点P1(x1,y1)、P2(x2,y2)在反比例函数y=$\frac{3}{x}$的图象上,当x1>x2>0时,下列结论正确的是( )
| A. | y2<y1<0 | B. | y1<y2<0 | C. | 0<y2<y1 | D. | 0<y1<y2 |
4.把弯曲的道路改直,就能缩短路程,其中蕴含的数学原理是( )
| A. | 过一点有无数条直线 | B. | 两点确定一条直线 | ||
| C. | 两点之间线段最短 | D. | 线段是直线的一部分 |
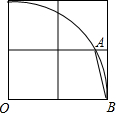 如图,在2×2的网格中,以顶点O为圆心,以2个单位长度为半径作圆弧,交图中格线于点A,则tan∠ABO的值为2+$\sqrt{3}$.
如图,在2×2的网格中,以顶点O为圆心,以2个单位长度为半径作圆弧,交图中格线于点A,则tan∠ABO的值为2+$\sqrt{3}$.