题目内容
14.-$\sqrt{3}$的相反数是$\sqrt{3}$.分析 根据相反数的定义,可得答案.
解答 解:-$\sqrt{3}$的相反数是 $\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题考查了实数的性质,在一个数的前面加上负号就是这个数的相反数.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
11.不等式4x-k≤0的正整数解是1,2,3,那么k的取值范围是( )
| A. | 12≤k<16 | B. | 12<k<16 | C. | 3≤k<4 | D. | 3<k≤4 |
9.计算-2x(x2-1)的结果是( )
| A. | -2x3-2x | B. | -2x3+x | C. | -2x3+2x | D. | -x3+2x |
4.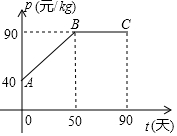 某公司购进一种商品的成本为30元/kg,经市场调研发现,这种商品在未来90
某公司购进一种商品的成本为30元/kg,经市场调研发现,这种商品在未来90
天的销售单价p(元/kg)与时间t(天)之间的相关信息如下图,销售量y(kg)与时间t(天)之间满足一次函数关系,且对应数据如下表.设第t天的销售利润为w(元)
(1)分别求出售单价p(元/kg)、销售量y(kg)与时间t(天)之间的函数关系式;
(2)问:销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)在实际销售的前50天中,公司决定每销售1kg该商品就捐赠n元利润(n<12)给“精准扶贫”对象.现发现:在前50天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
 某公司购进一种商品的成本为30元/kg,经市场调研发现,这种商品在未来90
某公司购进一种商品的成本为30元/kg,经市场调研发现,这种商品在未来90天的销售单价p(元/kg)与时间t(天)之间的相关信息如下图,销售量y(kg)与时间t(天)之间满足一次函数关系,且对应数据如下表.设第t天的销售利润为w(元)
| 时间t(天) | 10 | 30 |
| 每天的销售量 y(kg) | 180 | 140 |
(2)问:销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)在实际销售的前50天中,公司决定每销售1kg该商品就捐赠n元利润(n<12)给“精准扶贫”对象.现发现:在前50天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
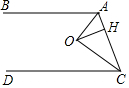 如图,AB∥CD,OA,OC分别平分∠BAC和∠ACD,OH⊥AC于点H,且OH=4,则AB,CD之间的距离为8.
如图,AB∥CD,OA,OC分别平分∠BAC和∠ACD,OH⊥AC于点H,且OH=4,则AB,CD之间的距离为8.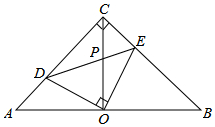 如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:①∠AOD=∠COE;②图形中全等的三角形有3对; ③△ABC的面积等于四边形CDOE的面积的2倍;④CD+CE=$\sqrt{2}$OA;⑤AD2+BE2=2OD2,其中正确的结论有( )
如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:①∠AOD=∠COE;②图形中全等的三角形有3对; ③△ABC的面积等于四边形CDOE的面积的2倍;④CD+CE=$\sqrt{2}$OA;⑤AD2+BE2=2OD2,其中正确的结论有( )
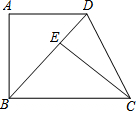 如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC.
如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC.